本稿では、ウエハ研磨をさまざまな観点で概説します。内容はできるだけ一般的な内容に留めるようにしますが、筆者の(短い!)経験は主にSiCウエハのCMP(Chemical Mechanical Polishing)における数値シミュレーションや機械学習の応用に関するものです。そのため、記事の一部ではこの分野に関連した例を取り上げています。また、読者の皆さまは半導体やその製造プロセスに関する基本的な知識をお持ちであることを前提としています。
本稿の構成は以下のとおりです:
まず、「ウエハ研磨の基礎」では、研磨プロセスの原理とその重要性について説明します。次に、「ウエハ研磨の課題」では、特にSiCのような硬質材料を高精度に研磨する際に直面する技術的課題について述べます。続いて、「ウエハ研磨へのAI応用例」では、近年のAI技術がウエハ研磨にどのように活用されているかを具体的に紹介します。最後に、「ウエハ研磨とプロセスインフォマティクス」では、ウエハ研磨プロセスがプロセスインフォマティクス(Process Informatics)と呼ばれる、製造プロセス全体の改善を目的としたアプローチにどのように統合されるかについて簡単に触れます。
ウエハ研磨の基礎
ここでは、特にCMP(化学機械研磨)を中心に、研磨の基本と、なぜ半導体において研磨が必要なのかについて簡単に説明します。本セクションの多くの情報は、Nishi & Doering(2008)1およびSuryadevara(2021)2に基づいています。
ウエハ研磨の概念と原則
人類は太古の昔から、実用的な目的のために物体の表面を平坦にする必要がありました。研削機や研磨機、サンダーなどは歴史を通じて常に作られており、技術の進歩とともに平坦化のための道具はより複雑で高度に特化されたものへと進化してきました。やがて、この進化は半導体製造専用の装置にもつながりました。これらの装置は非常に高精度であり、表面をおよそ0.1ナノメートルレベルで平坦にすることができます。
半導体においては、ウエハを平坦化する目的や精度に応じて、いくつかの異なる研磨方法が用いられています。そのため業界内では、以下のように用途ごとに異なる呼称が使われています。
- 研削(Grinding)… ウエハから大量の材料を迅速に除去する目的で用いられます。これは主に表面の破壊や引っかきによって機械的に削り取るものであり、研磨粒子が表面に埋め込まれたペレット状の砥粒を使用します。砥粒は研削対象の材料よりも硬いもの(例えばダイヤモンド砥粒)が使われます。
- ラッピング(Lapping)…研削によって生じた表面損傷を軽減し、より細かい全体的な平坦化を行うために使われます。基本原理は研削と同様ですが、ペレット状ではなく、より小さな研磨粒子を使用する点が異なります。
- 研磨(Polishing)…最も微細なレベルの平坦化を目的とした方法です。現在の半導体産業で最も一般的に使用されているのが、化学機械研磨(Chemical Mechanical Polishing, CMP)です。この方法では、機械的効果と化学的反応を組み合わせて材料を除去します。ポリッシャー(研磨装置)の内部にスラリーを供給し、ウレタンなどの弾性パッドを装備したポリッシャーでウエハ表面を処理します。スラリーにはウエハ表面と化学反応を起こして表面を軟化させる成分が含まれており、その軟化層をパッド表面が機械的に削り取ることで、ウエハ全体を均一に研磨します。
ここでは、平坦化プロセスの中でも研磨に焦点を当てて説明します。研磨の基本的な考え方は、ウエハと研磨装置の間に加えられる圧力と相対運動の組み合わせによって、材料が除去されるというものです。この関係は、Preston による古典的な式で表されます3:
\( MRR = k_p v_r P \)
ここで\( MRR \)は材料除去率(Material Removal Rate)、\( k_p \)は Preston 係数、\( v_r \)は研磨装置とウエハとの相対速度、\( P \)は圧力を意味します。\( k_p \)はプロセスの効率を決定する比例定数であり、非常に重要な役割を担います。
この係数には、\( v_r \)や\( P \)以外のあらゆる物理的要因や効果、たとえば温度、パッドの材料、スラリーの組成、スラリーのpHなどが含まれています。これまでにさまざまな修正バージョンの式が提案されており、\( MRR \)の\( v_r \)および\( P \)に対する線形依存性をより複雑なべき乗関係へと拡張したものや、もともと\( k_p \)に含まれていた変数を明示的に取り出した形式などが存在します。
しかし、式(1)は、本質的な関係を示しており、現在でも材料除去率を見積もるための基本的なモデルとして広く使われています。


Figure. 1(a)Single-side, single-wafer polisher4(b)Double-side, multi-wafers polisher5
この節の締めくくりとして、研磨に使用される装置について簡単に説明します。
ウエハに圧力と相対速度差を加える方法は装置ごとに異なり、さまざまな種類の研磨装置が存在します。中でも最も一般的なのは、ウエハ表面全体にできるだけ均一な研磨を実現するために、軌道運動(オービタルモーション)を用いるタイプです。
最も単純な構成では、ウエハの片面を研磨装置に押し当て、ウエハと研磨パッドの両方を異なる回転数で回転させることで研磨を行います(Figure 1a)。
さらに複雑な構成の装置では、複数枚のウエハを同時に、かつ両面を同時に研磨することが可能です(Figure 1b)。これらの装置では、ウエハをキャリアに配置し、遊星歯車(エピサイクリックギア)を使って移動させると同時に、上下の研磨パッドもそれぞれ独立して回転します。
半導体における研磨プロセスの役割と重要性
半導体におけるウエハ研磨の重要性、特にCMPを用いた研磨の重要性は、端的に言えば「半導体デバイス」のためです。現在存在するすべての集積ロジックデバイスやメモリデバイス(スマートフォン、ノートパソコン、自動車など、ここではほんの一部の例にすぎません)は、半導体デバイスを基盤としています。半導体デバイスの製造には複数の工程があり、その多くで高い平坦性を持つ表面が求められます。
以下に代表的な例をいくつか挙げます。
- 多層積層構造:半導体デバイスは、シリコンなどの基板上に複数の層を積み重ねて構成されます。この上には誘電体層や金属配線層などが順次形成されます。各層は、下層が平坦であることを前提に形成されるため、表面の凹凸が蓄積すると、ショートや接続不良、欠陥の原因となります。CMPは、各層を形成するたびに余剰材料を除去し、次の層を正確に積層できるように表面を平坦にします。
- 高精度リソグラフィ:現代の半導体デバイスは、フォトリソグラフィ(光をウエハに投影して回路パターンを描く技術)に依存しています。この際、表面に凹凸(バンプ、キズ、うねりなど)があると、ピントがずれたり、投影パターンが歪んだりして、不良や動作不良の原因となります。研磨によって平坦かつ均一な表面を確保することは、ナノメートルスケールでの高解像度パターン形成に不可欠です。
- 薄膜プロセス:異なる材料を半導体基板上に積層するために、原子層堆積(ALD)や化学気相成長(CVD)といった薄膜形成技術が使われます。これらすべてのプロセスでは、材料を均一に成膜するために滑らかな基板表面が必要です。研磨を行わなければ、成膜された層にボイド(空隙)やピンホール、厚さのばらつきが生じ、電気的な不具合につながります。
- 微細化への対応:半導体技術がスケーリングによって微細化するにつれて、表面の平坦性の重要性はますます高まっています。現在の技術では、トランジスタの寸法(ノード)は1ナノメートルに迫っており、このようなスケールでは、わずかな高さの違いも重大な問題となります。このため、サブナノメートルレベルの平坦性を確保できるCMPのようなプロセスは、さらなる微細化を可能にするために不可欠です。
- デバイス性能の向上:一般に、表面の不均一性はウエハ全体の電気特性のばらつきを生じさせ、性能の一貫性や歩留まり(1枚のウエハから得られる良品数)を低下させます。
上で述べた点に加えて、ウエハ研磨は、SiCのようなワイドバンドギャップ材料を用いた半導体の製造において特別な役割を果たします。これらの材料は非常に硬く、結晶構造の性質上、もともと表面が粗くなりやすいという特徴があります。そのため、切断や研削などの加工工程で生じる欠陥が除去しにくく、高性能なデバイスを実現するには、効果的なCMPプロセスが不可欠です。
ウエハ研磨における課題
このセクションでは、CMPプロセスにおける主な課題について説明します。特に、SiCのような加工が困難な材料に焦点を当てて述べます。本セクションも、Nishi & Doering(2008)[1]および Suryadevara(2021)[2]の記述に基づいています。
全体および局所的な平坦性の改善
前のセクションで述べたとおり、ウエハにおいては、表面が平坦であるほど望ましいとされています。ただし、平坦性には2つの異なるレベルがあります。「全体の平坦性(global planarisation)」とは、ウエハ全体を見たときの平坦さを指し、たとえば表面全体にわたる歪みや、特定の領域が他よりも過剰に研磨されているといった傾向を含みます。一方、「局所の平坦性(local planarisation)」は、ウエハ表面の微細なレベルでの欠陥(たとえばキズ)や、微小な凹凸などを意味します。CMPは、半導体製造工程の最終段階に位置するプロセスであるため、最も厳しい平坦性の要求が課されます。そのため、全体および局所の両方の平坦性を最小限の変動に抑えることが極めて重要です。
全体の平坦性に関しては、ウエハの凹凸を生じさせる要因が多く存在します。よく見られる原因として、以下のようなものが挙げられます。
- 振動高調波(Vibration harmonics)…これは、現在最も一般的に使用されている軌道型研磨装置(orbital-type polisher)に特有の現象であり、ウエハを保持するキャリアと研磨パッドとの間の回転同期の影響を受けます。振動高調波は通常、スポーク状のパターンとして研磨レートの不均一性を引き起こします。この影響を防ぐために、キャリアは通常、テーブルに対して一定の周波数差で駆動されます。
- 端部の研磨ムラ(Non-uniform edge removal)…ウエハの端部では除去率が高く、中心に向かうにつれて徐々に低下していくパターンを指します。これは、キャリアの高速回転がテーブルの回転に対して優位になることで発生します。この効果は、両者の回転周波数を適切に調整することで緩和することができます。
ご想像のとおり、全体の平坦性に影響を及ぼす要因は、プロファイル制御(profile control)によって対処することができます。これは、CMPにおける研磨レートの均一性を実現するために、すべての加工パラメータを最適化する技術です。
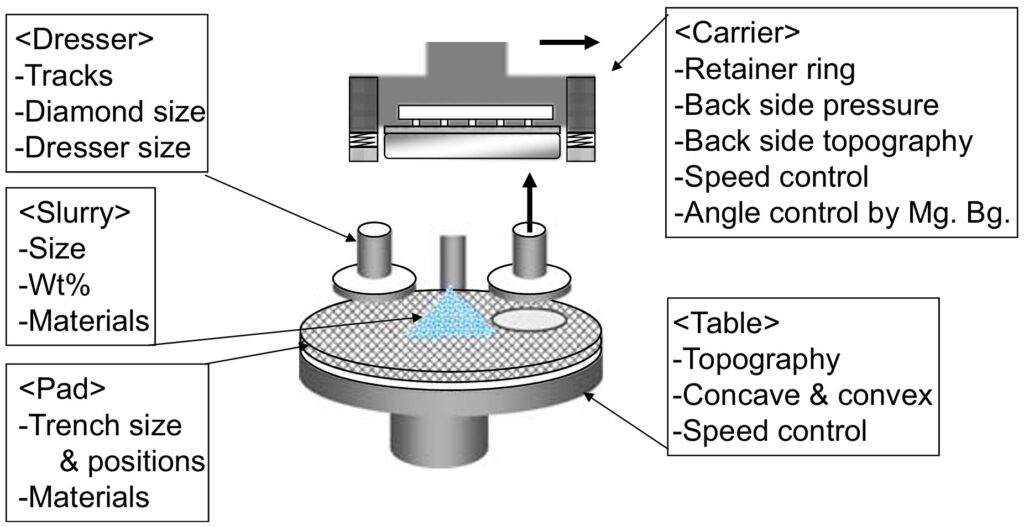
Figure 2 では、プロファイル制御に用いられる代表的な加工パラメータと、それぞれが対応する研磨装置の構成要素を示しています。ここでは、Figure 2 に示した各パラメータの詳細には立ち入りませんが、重要な点は、CMPプロセス制御には多数のパラメータが関与しており、接触力学や流体力学といった物理学の異なる分野や化学の知識が必要となるということです。したがって、プロセス制御は決して容易な作業ではありません。
局所の平坦性について考える際には、CMPによってウエハがどの程度の精度で研磨されるかを考慮しなければなりません。たとえば、研磨されたSiCウエハの表面粗さは通常、数マイクロメートルの一部に過ぎませんが、最も良好な場合には約0.5ナノメートルという極めて滑らかな表面に達することもあります。そのため、それを超える高さや深さの微細な突起や凹みは、すべて欠陥と見なされます。このような欠陥は、主に次の3つのカテゴリーに分類されます。
以下では、それぞれについて詳しく説明します。
- 異物および研磨残渣(Foreign materials and polish residues)…これは、ウエハの表面から突き出す形で現れる欠陥です。典型的な例としては、CMPで使用される研磨パッドやスラリーからの残渣、あるいはそれ以前の製造工程から引き継がれた残留物などがあります。この種の局所的欠陥は、ウエハ表面を適切に洗浄することで最小限に抑えることができます。
- キズ(Scratches)…これは、ウエハの表面に食い込む形で現れる欠陥です。前述の異物残渣よりも厄介であり、洗浄で除去することはできず、基本的には予防が唯一の対策となります。CMP中の機械的摩耗によって発生し、ウエハ表面に接触するあらゆる材料や界面がキズの原因となり得ます。典型的な原因としては、スラリー中の研磨粒子がパッドとウエハの間に挟まってしまうことや、研磨粒子の蓄積などが挙げられます。これらの欠陥は主に、パッドとウエハの間にスラリーが適切に流れるよう制御することで防止されます。
- 腐食および化学的攻撃(Corrosion and chemical attack)…これも、ウエハの表面に食い込む形の欠陥です。CMPは化学的プロセスでもあり、スラリーとの反応によりウエハ表面が軟化します。このため、もともと表面に減算的な欠陥を有している箇所は、スラリーの化学成分が局所的に蓄積しやすくなり、ピット(くぼみ)として欠陥が進行する原因になります。この場合も、パッドとウエハの間でスラリーの流れを適切に保つことで、欠陥の発生を抑えることができます。
局所的な平坦性に悪影響を及ぼす要因は、全体の平坦性に影響する要因よりも予測が難しく、それらを体系的に防止するのも困難です。したがって、研磨装置を常に清潔に保ち、完璧な動作状態を維持することによって、これらの欠陥をできる限り抑えることが求められます。
難加工材料に対する研磨速度の向上
2010年代初頭以降、半導体研究の関心は、SiCのようなワイドバンドギャップ材料へと移りつつあります。これらの材料は、高温環境下でSiに代わる可能性を秘めており、Si製デバイスでは正常に動作しなくなる条件下でも使用が可能です。CMPの観点から見た場合、SiCの課題はその非常に高い硬度にあります(SiCは地球上で3番目に硬い化合物であり、ダイヤモンドおよび炭化ホウ素に次ぐ硬さです)。このため、SiCは非常に研磨しにくい材料です。
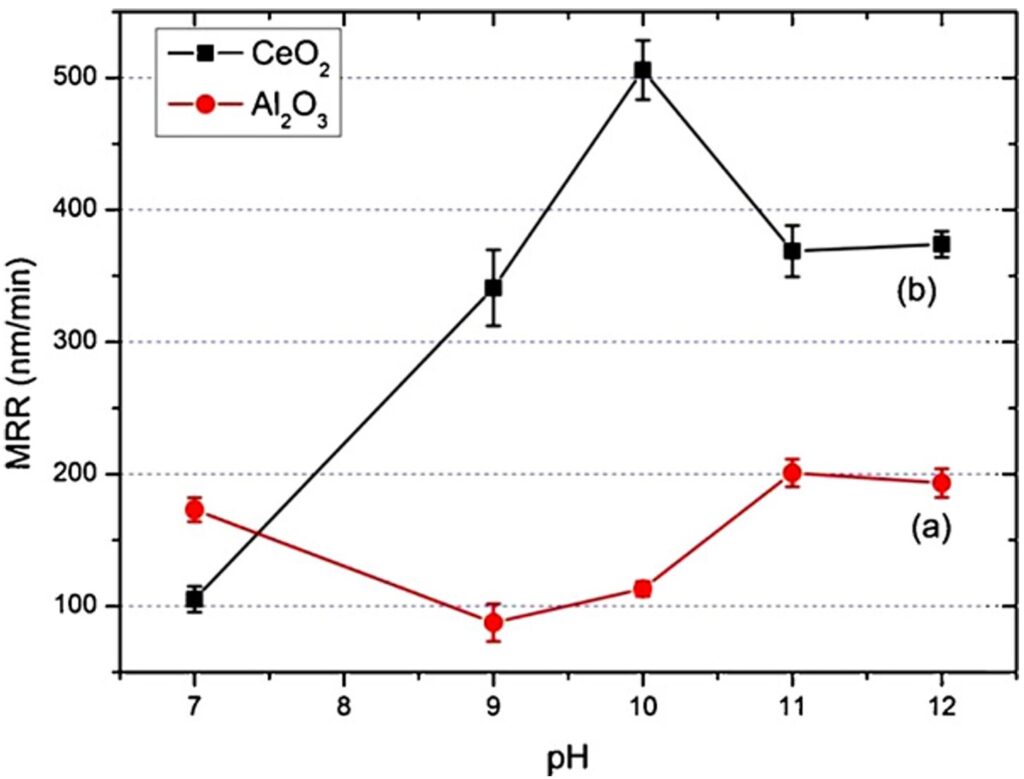
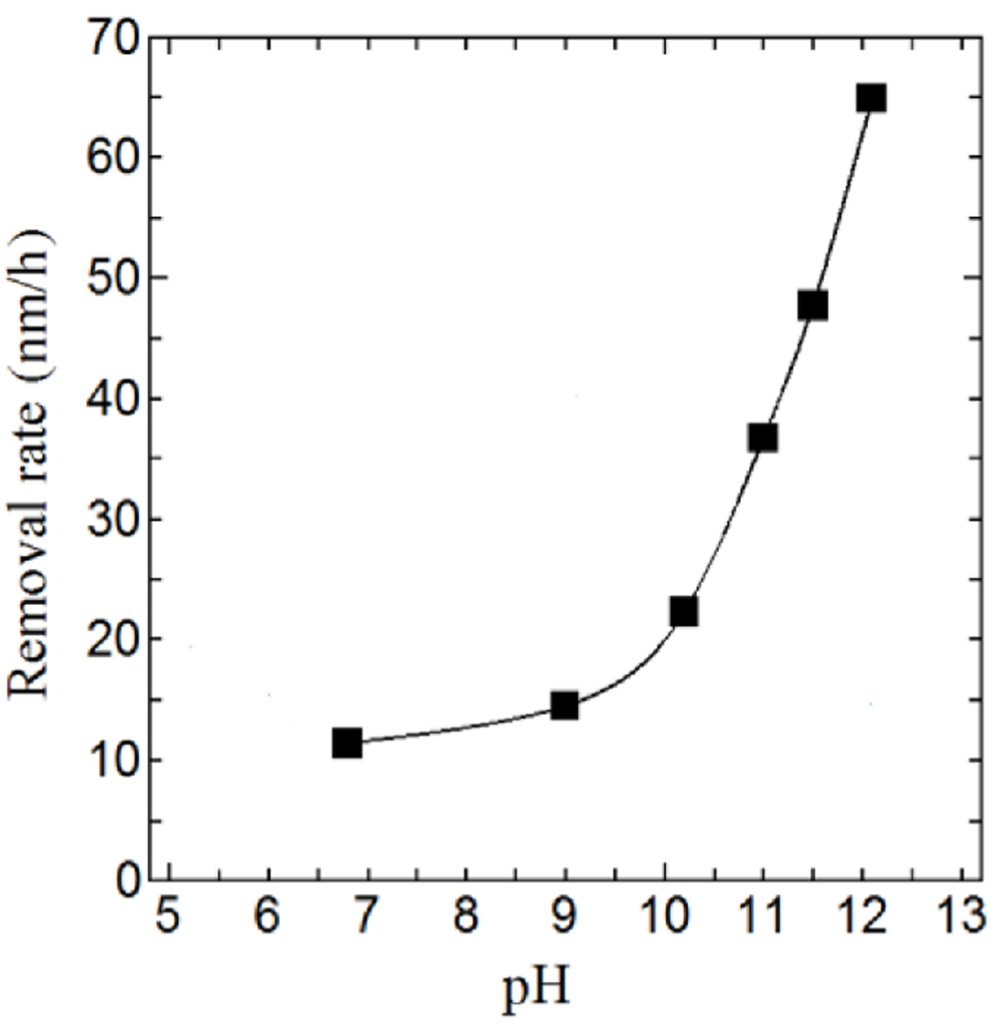
Figure 3: MRR as a function of the slurry Ph for Si (a), from Wang et al. 2011, and for SiC (b), from Yin et al. 2018.
比較として、Figure 3 にスラリーのpHに対する研磨レート(MRR)の変化を示します。図の (a) はSi、(b) はSiCの例です。Siの平均的なMRRは数百nm/minであるのに対し、SiCは数十nm/minにとどまり、一桁の差があります。当然ながら、研磨にかかる時間もSiCの方がはるかに長くなります。SiCが半導体市場で競争力を持つためには、他の要素とともに、このMRRを改善することが不可欠です。そのため、実験的アプローチとシミュレーションによるアプローチの両方が活用されています。実験的な側面では、スラリーの改良に多くの注目が集まっています。
実験的なアプローチにおいては、スラリーのエッチング特性に大きな関心が寄せられています。というのも、式(1)に示すように圧力や相対速度を増加させるだけでは、ウエハの表面がスラリーとの化学反応によって適切に軟化されていない限り、十分な効果を得ることができないためです。現在、有望とされているスラリーの組成の多くは酸化物ベースであり、過酸化水素(H₂O₂)や過マンガン酸カリウム(KMnO₄)などの酸化剤を含んでいます。これらのスラリーは、ウエハ表面に大きな副作用を与えることなく、最大で約30 nm/minのMRRを実現することが可能です。さらに、この種のスラリーは、無研磨粒子(abrasive-free)、すなわちスラリーに研磨粒子を一切混合しない状態でも高いMRRを達成する傾向があることが報告されており、キズなどの表面損傷を低減するうえでも有効であるとされています。
シミュレーションによるアプローチは、実験とは異なる方向性を取っており、圧力・相対速度・研磨時間といった加工パラメータの微調整によってMRRを向上させることを目的としています。この方法の利点は、実験に比べて低コストかつ短時間で実行できるため、実験を効率的に導く手段として活用できる点にあります。CMPのシミュレーションでは、通常、有限要素法(finite element method, FEM)を用いてPrestonの式(1)を離散的な時間ステップごとに数値的に解きます。これは、実験に使用される装置の形状に基づいて構築された計算グリッド上で行われます。このアプローチの基本的な考え方は、Preston係数(\( k_p \))を基礎的な実験データセットを使ってキャリブレーション(調整)したうえで、相対速度(\( v_r \))、圧力(\( P \))、研磨時間などのパラメータを自由に変動させることで、広範囲の加工条件を仮想的に探査できるという点にあります。これは、Prestonの式の議論で述べたように、\( k_p \)が化学的影響、パッドの硬さ、研磨粒子のサイズ、スラリーの化学組成など、さまざまなプロセス条件や消耗品、装置パラメータの影響を含んでいるためです。したがって、\( v_r \)・\( P \)・研磨時間以外の実験条件が一定であれば、シミュレーション結果は妥当性を持ち続けます。さらに、サーバーやスーパーコンピュータ上で複数のシミュレーションを並列実行することができ、数千通りの加工条件を数日程度で探索することも可能です。
ウエハ研磨へのAI適用事例
本稿執筆時点、すなわち2025年初頭には、AI(人工知能)はすでに数年にわたって広く普及しています。それは日常生活だけでなく、ほぼすべての研究分野にも影響を与えており、ウエハ研磨の研究分野にもAIが取り入れられつつあります。
このセクションでは、ウエハ研磨分野におけるAI活用の例として、材料除去率(MRR)の予測とウエハ欠陥の予測・検出という2つの事例を紹介します。前者の代表的な例としては Wang らの研究6を、後者の事例としては Kim & Behdinanによる研究7を取り上げます。
深層学習による材料除去率(MRR)の予測
前のセクションでも述べたように、CMPの数値シミュレーションは、実験よりも高速かつ低コストであるため、実験の指針として活用できます。しかし、数値シミュレーションよりもさらに高速なのがAIモデルです。比較すると、SiCウエハの標準的な研磨時間は10〜20時間ですが、数値シミュレーションは数時間で完了し、AIモデルによる予測は1分未満で実行できます。このことから、CMPの結果をAIで予測することには大きな利点があります。さらに、AIモデルは、物理方程式に基づく数値シミュレーションでは考慮が難しい多数のパラメータの影響を取り込むことができるという利点もあります。この分野の研究が加速したきっかけの一つは、2016年のPrognostics and Health Management(PHM)データチャレンジです。このチャレンジでは、実験データに基づいてCMPのMRRを予測する課題が出され、多くの研究者がさまざまなAIアルゴリズムを用いてCMP予測を試みるようになりました(e.g., Wang et al. 2017[6], Di et al. 20178, Yu et al. 20199, Liu et al. 202210, Lv et al. 202311, Wei &Wu 202412 )。ただし、それらの多くはわずかな精度向上のために、過度に複雑で過剰設計された手法を採用している傾向が見られます。これはAI研究においてよくあることです。
そこで本稿では、最も古い研究の一つではありますが、シンプルなアプローチで高い予測精度を達成している Wang らの研究[6]を取り上げて紹介します。
Wang らは、材料除去率(MRR)とプロセスパラメータの複雑な関係をモデル化するために、深層信念ネットワーク(Deep Belief Network, DBN)を使用しています。DBNは、特徴量間の非線形な関係を捉えるのが得意であり、確率的な出力(予測値に対する信頼度の幅)を得ることも可能です。
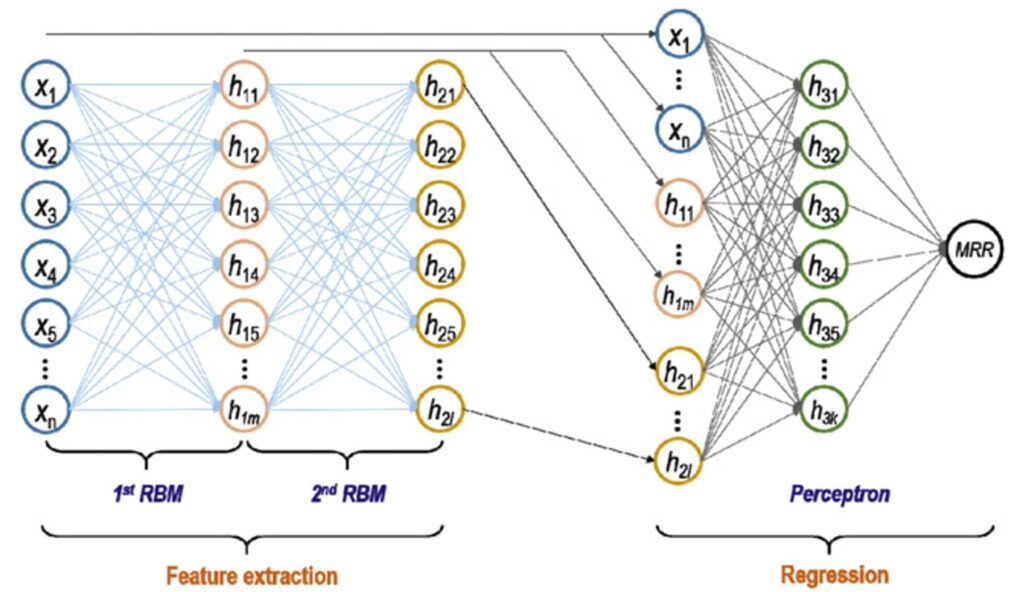
Image taken from the publication
Figure 4 に彼らのDBNの構造が示されています。ネットワークは大きく2つの部分から構成されています。1つは制限ボルツマンマシン(Restricted Boltzmann Machines, RBMs)を積み重ねた部分、もう1つはパーセプトロン(perceptron)です。それぞれの機能と配置について説明します。
- 積層RBM(Stacked RBMs)…この部分の役割は、モデル内の特徴量間に存在する未知かつ複雑な関係性(パターンや潜在特徴など)を学習することです。何を探しているかが事前にわからないため、RBMの訓練は教師なしで行われます。Figure 4 の左側に示されているように、2層のRBMが使用されています。1層目のRBMは入力特徴量(X₁, …, Xₙ)を処理し、2層目のRBMは1層目の出力を処理します。それぞれのRBMは、隠れ層(h₁₁, …, h₁ₘ)、(h₂₁, …, h₂ₗ)を通じてデータを表現し、入力特徴を高次元空間に変換することで、データに内在する隠れたパターンを明らかにする能力を高めます。このようにRBMを積み重ねることで、Wang らは元の特徴量を多段階の高次元表現として扱い、データパターンの抽出精度を最大化することを目指しています。
- パーセプトロン(Perceptron)…この部分の役割は回帰処理を行い、MRRを予測することです。このネットワークは順伝播型の全結合ニューラルネットワークであり、以下の3層で構成されています:
- 入力層:元の特徴量(X₁, …, Xₙ)と、RBMによって得られた高次元の特徴量(h₁₁, …, h₁ₘ, h₂₁, …, h₂ₗ)から構成されます。
- 隠れ層:第3の中間層として新たに構成される(h₃₁, …, h₃ₖ)。
- 出力層:最終的にMRRを表現するノードです。
さらに、このネットワークの教師なし学習部分における重みと学習率は、粒子群最適化(Particle Swarm Optimization, PSO)アルゴリズムを用いて最適化されています。詳細な仕組みは本稿の範囲を超えますが、目的はMRRの回帰誤差を最小化するパラメータの組み合わせを見つけることにあります。
続いて、この研究で使用された特徴量と結果について説明します。予想されるとおり、特徴量としてはCMPプロセス中に測定された各種の加工パラメータおよび研磨装置の各構成部品の摩耗データが使用されています。これらは、プロセスの異なる時点で取得され、使用状態・圧力・速度の3カテゴリに分類された計16項目の特徴量から構成されています(Table 1)。
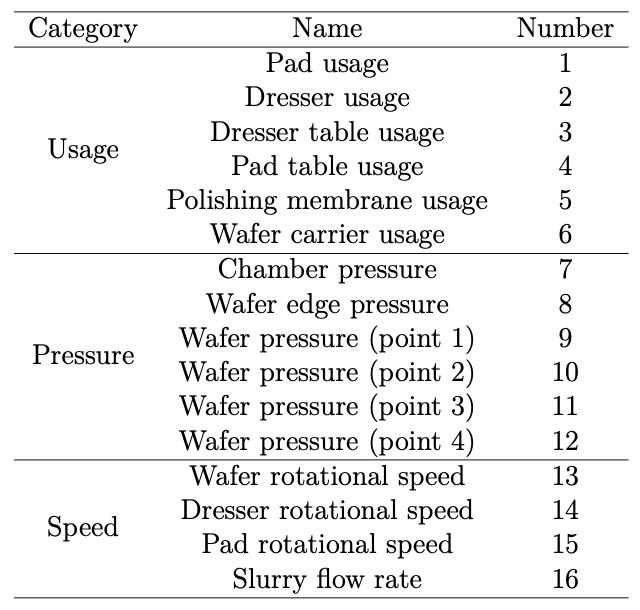
これらの特徴量は非常に多岐にわたり、それらの相互関係を人間が把握したり、物理モデルとして数式化したりすることは困難です。Table 1 に示された全ての特徴量は、2398枚のウエハに対して取得されており、そのうち1975枚が学習用、423枚がテスト用として使用されました。
このデータに基づいてDBNを学習させた結果、WangらはMRRのRMSE(平均二乗誤差平方根)として2.7 nm/minを達成しました。これは、他のネットワークと比較してわずかに優れた精度であり、たとえば誤差逆伝播型ニューラルネットワーク(BPNN)では3.3 nm/min、サポートベクター回帰(SVR)では3.1 nm/minのRMSEが得られています。
この研究の詳細に加えて、最も重要なポイントは、CMPのパラメータ空間があまりにも広く複雑であり、物理方程式によって効率的に探索することは現実的ではないという点です。したがって、そこに存在する隠れた非線形で複雑な関係性を理解するには、モデルが適切に構築され、学習されている限りにおいて、AIの活用が唯一の有効な手段となります。
AIを用いたウエハ欠陥の認識と検出
このセクションでは、ウエハの欠陥検出および分類に関するさまざまな手法について紹介します。特に、機械学習および深層学習に基づく手法に焦点を当てます。参考文献である Kim & Behdinan による論文13は、独自の研究というよりも、この分野に関する包括的なレビュー論文です。したがって、ここでは彼らの論文に記載された主要なポイントを要約して紹介します。詳しく知りたい場合は、ぜひ原論文をご参照ください。
ウエハの欠陥検出にAIを用いる必要性は、現在のウエハ製造における極めて高い精度に起因しています。集積回路が小型化することで、欠陥のスケールも小さくなり、欠陥の複雑性や発生頻度が増加しています。このような状況下では、もはや手作業による欠陥検査は現実的ではなく、AIの活用が不可欠となります。特に、欠陥のパターンが多様化する中で、原因分析(root-cause analysis, RCA)の重要性が飛躍的に高まっています。RCAとは、欠陥をその発生メカニズムに基づいて分類・分析するプロセスです。なお、「全体および局所の平坦性の改善」で主要な欠陥要因についてはすでに説明しましたので、ここではAIによるウエハ欠陥検出の主な活用方法と現在の課題に焦点を当てて述べます。教師あり学習(supervised learning)によるウエハ欠陥検出は、ラベル付きデータを用いることで比較的低い計算コストで高精度な判別が可能ですが、以下のような課題も抱えています。
- データの制約(Data Limitations)…ラベル付きデータ(すなわち、各欠陥に対してその種類や発生原因が明示されているデータ)は入手が困難であり、また取得コストも高いため、実環境でのモデルの拡張性に限界があります。
- 過学習(Overfitting)…欠陥の種類ごとにデータの数に偏りがあると、モデルは多数派クラスに引きずられ、少数派の欠陥を誤分類する傾向があります。特に、欠陥の見た目が似ている場合、この問題は顕著になります。
これらの課題に対処するため、研究者たちはデータ拡張や特化型の深層学習手法を用いて、特徴量の学習精度を向上させようとしています。しかし、これらのアプローチには、計算コストの増大、汎化誤差の増加、および複数の発生源に由来する欠陥の検出精度の限界といった欠点があります。
一方、教師あり学習とは異なり、教師なし学習(unsupervised learning)は、ラベル付けされていないウエハマップの豊富なデータを活用することができ、同等レベルの性能を達成できる可能性があります。しかしながら、教師なし手法にも以下のような制約があります。
- パラメータへの感度(Sensitivity to parameters)…ウエハ欠陥検出でよく使用されるクラスタリングアルゴリズムは、カーネル法、初期値、ハイパーパラメータなどに大きく依存しており、良好な性能を得るには慎重なチューニングが必要です。
- 計算コストの高さ(High computational complexity)…多くの教師なし手法は計算コストが高く、推論速度が遅いために実行時間が長くなるという課題を抱えています。
全体として、教師なし学習はウエハ欠陥の分類において有望な手法ではありますが、性能と計算効率のバランスを取るための効果的な戦略が求められます。
最後に、半教師あり学習(semi-supervised learning)は、ラベル付きデータとラベルなしデータの両方を組み合わせて、教師あり・教師なし両方の手法の限界に対応しようとするものです。ただし、このアプローチにも以下のような主要な制約があります。
- 計算コスト(Computational costs)…深層生成モデル(deep generative models)などの手法は、潜在表現の学習やデータ生成において非常に有効とされていますが、計算コストが非常に高く、教師あり学習や教師なし学習を上回る場合もあります。
- 研究の少なさ(Limited research)…有望な結果が報告されているにもかかわらず、半教師あり学習は教師あり・教師なしの手法に比べて研究例が少ないのが現状です。これは、手法自体の複雑さが一因であると考えられますが、裏を返せば、今後の研究開拓に向けた大きな可能性が残されているとも言えます。
まとめると、ウエハ欠陥検出におけるAIベースの手法は、欠陥の複雑化やデバイスの微細化に伴う課題に対して、非常に強力な解決策を提供します。教師あり学習、教師なし学習、半教師あり学習のいずれのアプローチにもそれぞれの強みがありますが、一方でデータの入手性、計算コスト、パラメータ感度といった本質的な制約も抱えています。
今後は、深層学習アーキテクチャの進化、データ拡張戦略の高度化、およびハイブリッド手法の開発が、これらの課題を克服し、半導体製造における欠陥検出の精度と効率をさらに向上させるうえで重要な鍵となります。
ウエハ研磨とプロセスインフォマティクス
最後に、このセクションではプロセスインフォマティクス(PI)の概念と、それがウエハ研磨とどのように関係するかについて簡単に説明します。
プロセスインフォマティクスとは?
PI(プロセスインフォマティクス)という用語は、マテリアルズインフォマティクス(MI)の考え方に由来しています。MIとは、材料の理解、利用、選定、開発、発見を目的として、情報科学やデータサイエンスの原理を材料科学・材料工学に応用する研究分野です。
これと類似して、PIは以下のように定義されています。「近年著しく進展したデータ科学と、実験科学・理論科学・計算科学を統合的に活用し、目標とする材料の合成プロセスを効率的かつ統合的に探索するための手法」(引用元:革新的材料創成技術のためのプロセス科学基盤)。
より平易に言えば、PIとは製造プロセスの最適化手法です。情報科学の力を活用し、製造装置の構成、加工・物理パラメータ、消耗部品の組み合わせなど、最適な製造条件を高速に見つけ出すアプローチです。これにより、開発期間を大幅に短縮することができます。
PIの詳細な解説については、当社の技術ブログに掲載された以下の記事をご参照ください:
「【プロセスインフォマティクス入門】製造プロセス最適化のための情報技術を易しく解説」
ウエハ研磨へのプロセスインフォマティクスの応用
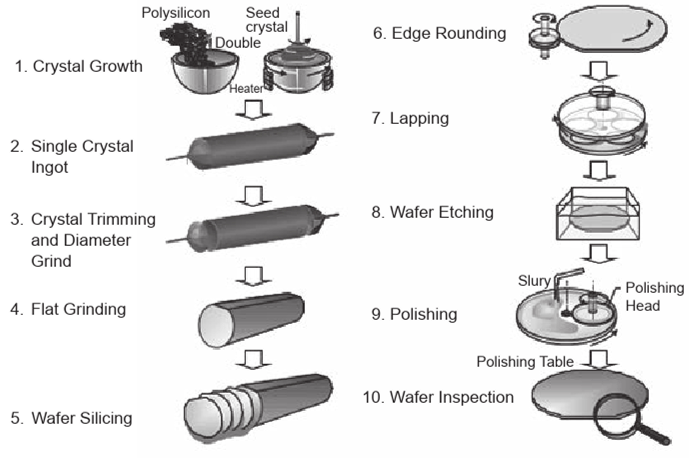
ウエハの加工工程は、Figure 5 に示されるように、非常に多くの製造ステップから構成されており、プロセスインフォマティクス(PI)はその最適化手法として非常に適しています。実際、Figure 5 に示された各ステップは完了までに数時間(中には10時間以上かかる工程もあります)を要し、機械の稼働や材料の使用といった観点でも大きなコストがかかります。
そのため、加工条件の最適化不足や誤った消耗品の使用といった些細なミスでも、時間とコストの両面で大きな損失につながります。これらのステップのいずれか、あるいはすべてに対してPIを用いて最適化できれば、AIによる仮想実験によって数分以内に最適な条件を導き出すことも可能になります。
しかし、このように各工程の最適化結果を次工程の入力として順次利用していく「カスケード型の最適化」アプローチには、2つの大きな課題があります:
- 誤差の蓄積…「ウエハ研磨へのAI応用例」で述べたとおり、AIモデルは完全ではなく、実験結果をある程度の精度で予測するものです。したがって、ある工程における予測が誤っていた場合、その影響は後続のすべての予測に波及し、誤差が累積していくという問題が生じます。
- 完全なデータセット…PIに必要なのは、単なる大量の「ビッグデータ」ではなく、問題を解くのに十分な情報を持ったデータです。AIモデルは学習に使用されたデータのパターンを近似するため、学習データが存在しない領域では予測精度が大きく低下します。また、十分なバリエーションを持ったデータが必要です。ある領域のデータが希薄であれば、その近傍での予測精度は必然的に悪化します。
上記の2つの検討事項のうち、最初の「誤差の蓄積」は、ウエハ研磨において特に重要な問題となる可能性があります。なぜなら、ウエハ研磨は加工シーケンスのかなり後半(Figure 5 に示すステップ9/10)に位置するためです。しかし、前工程の予測結果に由来する誤った入力データへの対処方法について議論することは、本稿の範囲を超えます。そこでここでは、2つ目の「データの不十分さ」に焦点を当てます。
ウエハ研磨に関する実験データの取得は困難です。第一に、多くの企業がそれらのデータを独自ノウハウとして保有しており外部に公開されないこと、そして第二に、測定そのものに時間と労力がかかることがその主な理由です。その結果、AIモデルのパラメータ最適化に十分な多様性と網羅性を持ったデータセットを構築することは容易ではありません。
しかし、この課題に対しては、物理シミュレーションとAIとの相乗効果が非常に有効な解決策になる可能性があります。物理シミュレーションを実験データでキャリブレーションすることで、AIモデルを高精度な合成データで学習させることができ、実測データの不足という制約を克服できます。AIはデータからパターンを推論する手法であるのに対し、物理シミュレーションは基本法則に基づいており、実験条件に合わせて調整されるため、より堅牢です。たとえばCMPでは、ある研磨パッドやスラリーの種類、温度といった条件に対してPreston係数(式(1))を一度キャリブレーションすれば、圧力や相対速度の任意の組み合わせに対する結果をシミュレーションで予測できます。このように、物理シミュレーションはAIモデルほど多くのデータを必要とせず、それでいて高い精度を維持できるという利点があります。
実験データ、物理シミュレーション、そしてAIによる最適化を組み合わせることで、ウエハ研磨におけるプロセスインフォマティクスの可能性が大きく広がり、より効率的で高精度、かつデータ駆動型の製造が実現される道が開かれます。
アイクリスタルはプロセスインフォマティクスのプロフェッショナル集団です。
当社の技術やソリューションに関心をお持ちの方は、ぜひ当社のホームページで詳細をご確認ください。製造業におけるPIの最適なパートナーとして、皆様のご期待に応えます。
お問い合わせはこちら:お問い合わせフォーム
お気軽にご連絡ください。
参考文献
- Nishi, Y. & Doering, R., eds. 2008, Handbook of Semiconductor Manufacturing Technology, 2nd edn. (CRC Press) ↩︎
- Suryadevara, B., ed. 2021, Advances in Chemical Mechanical Planarization (CMP), 2nd edn. (Elsevier) ↩︎
- Preston, F. 1927, J. Society of glass Tech., 11, 214 ↩︎
- Yang, X., Yang, X., Aoki, K., & Yamamura, K. 2023, Precision Engineering, 83, 237 ↩︎
- Unitech Co., Ltd https://unitech-net.jp/en/ ↩︎
- Wang, P., Gao, R. X., & Yan, R. 2017, CIRP Annals, 66, 429 ↩︎
- Kim, T. & Behdinan, K. 2023, Journal of Intelligent Manufacturing, 34, 3215 ↩︎
- Di, Y., Jia, X., & Lee, J. 2017, International Journal of Prognostics and Health Management, 8, 31 ↩︎
- Yu, T., Li, Z., & Wu, D. 2019, Wear, 426-427, 1430, 22nd International Conference on Wear of Materials ↩︎
- Liu, C.-L., Tseng, C.-J., Hsaio, W.-H., Wu, S.-H., & Lu, S.-R. 2022, Applied Sciences, 12 ↩︎
- Lv, C., Huang, J., Zhang, M., Wang, H., & Zhang, T. 2023, Sensors, 23 ↩︎
- Wei, Y. & Wu, D. 2024, Journal of Intelligent Manufacturing, 35, 115 ↩︎
- Kim, T. & Behdinan, K. 2023, Journal of Intelligent Manufacturing, 34, 3215 ↩︎