製造業において製造プロセス最適化は言うまでもなく重要で、最適化を支える技術としてCAEなどが浸透していきました。しかしながら、複雑な物理現象になるとCAEの計算時間が長くなり、肝心の最適化考察に利用できないこともあります。このようなCAEの課題を解決するために、サロゲートモデルの活用も近年検討されていることは、本テックブログのプロセスインフォマティクス入門の記事で紹介した通りです。本記事では「物理を加味したサロゲートモデル」という一風変わった手法を紹介します。
サロゲートモデル×物理とは | 利点と方法
サロゲートモデルに物理を加味する利点
そもそも、一般的なサロゲートモデルはデータから法則を帰納的に学習するモデルであるため、物理的知識は不要にも思えます。しかしながら、学習に物理を加味することのメリットとして以下の点が述べられています。
- サロゲートモデルの物理的信頼性
- 少量のデータやノイズを含むデータでも対応可能
- 高い汎用性
以下順に解説します。
サロゲートモデルの物理的信頼性
後述するように、物理を加味したサロゲートモデルの中には、支配方程式の残差を誤差関数に用いる手法があります。この場合、残差を最小化するようにサロゲートモデルは学習するため、最終的に得られる結果も物理的に尤もであることが期待できます。一方でデータのみから学習するサロゲートモデルは物理を加味しないため、物理的妥当性は前者と比べ低いと考えられます。サロゲートモデルの結果から物理的考察をしたい場合は、物理の加味を検討すべきかもしれません。
少量のデータやノイズを含むデータでも対応可能
一般的にサロゲートモデル然りAIの学習には多数のデータが必要と言われます。データ数が少ない場合、モデルの精度は低く、データに無かったような入力に対する推論結果は正解から大きくずれてしまったりします。これに対して物理を加味した場合、データ以外にもヒントとなるものがあるため、精度向上が期待できます。
また、データに含まれるノイズは学習を妨げる原因となり得ます。このノイズは、言うならば注目している物理現象と関係ないものなので、前述のように支配方程式の残差をもとに学習すれば、ノイズによる悪影響の抑制が期待できます。
高い汎用性
後ほど紹介するように、物理的作用(例えば流体の乱流応力や非線形連続体の構成方程式)を学習する手法も提案されています。学習により得られたモデルは物理現象の基本要素に関するものなので、非常に汎用性が高いです。例えば、ある製品形状におけるCAE結果を予測するサロゲートモデルの場合、製品形状を入力データとして入れることが一般的ですが、作用素を学習したモデルは製品形状に依らず予測します。このようなモデルは様々な製品形状に対応可能なサロゲートモデルとなることが期待できます。
サロゲートモデルに物理を加味する方法
どのようにサロゲートモデルに物理を加味させることができるのか、その手法を紹介します。
- 誤差関数に支配方程式の残差を加える。
- 物理現象に即したモデルアーキテクチャを採用する。
- CAEのアルゴリズムのうち、特に計算時間を要する箇所のみAIで代替する。
以下順に解説します。
誤差関数に支配方程式の残差を加える
CAE解析でも登場する残差を誤差関数として利用します。残差が小さくなるように学習を進めるため、学習後のサロゲートモデルは支配方程式をある程度満たすことが期待できます。一般的な支配方程式は偏微分方程式で表現されますが、物理量の偏微分値は自動微分もしくはCAEと同様の方法で計算します。
物理現象に即したモデルアーキテクチャを採用する
対象としている物理によってはサロゲートモデルのアーキテクチャに工夫を凝らすことができます。例えば線形な物理現象の場合、重ね合わせの原理の利用は非常に有効です。顕著に現れるモードが少ないと事前に分かっているのであれば、各モードを別々に予測し、最終的な解はそれらを足し合わせる、といったアーキテクチャが考えられます。
CAEのアルゴリズムのうち、特に計算時間を要する箇所のみAIで代替
連続体力学のCAEの場合、よく内力の計算が問題になります。特に乱流応力や一部構成方程式には、CAEモデルの妥当性を保証するために細かい計算格子を必要とし、その結果計算時間が長くなります。そこで、CAEアルゴリズムの大体はそのまま採用しつつ、内力計算の部分のみサロゲートモデルで代替する手法が提案されています。
サロゲートモデル×物理の具体例の紹介
Physics Informed Neural Networks(PINNs)
Physics Informed Neural Networks(PINNs)とは、2019年にRaissi1らによって提案された手法で、MLPを用いて物理場を予測する手法です。サロゲートモデルの入力に時空間座標を採用している点が特徴であり、そのおかげで自動微分による支配方程式の残差評価が可能となっています。
PINNsの長所として以下の点が挙げられます。
- 実装が容易。支配方程式によるネットワークアーキテクチャの制約がない。
- 一般的なCAEと異なり、計算格子が不要。
- 支配方程式のみから学習することも可能で、データの準備が不要。
- 物理状態の時間発展について、CAEと違い逐次的に時間進行する必要がない。
一方でPINNsの欠点として、支配方程式が変わる度に再学習が必要な点が挙げられます。例えば \( u \)に関する偏微分方程式が \( N[u] = S \)で表されるとします。ここで\( S \) はソース項です。もし様々な\( S \)における上式の解を求めたい場合、PINNsはその値毎に学習しなければなりません。これは一般的なCAEでも言えることですが、劇的な高速化を期待してサロゲートモデルを検討している方にとっては欠点と言えるでしょう。
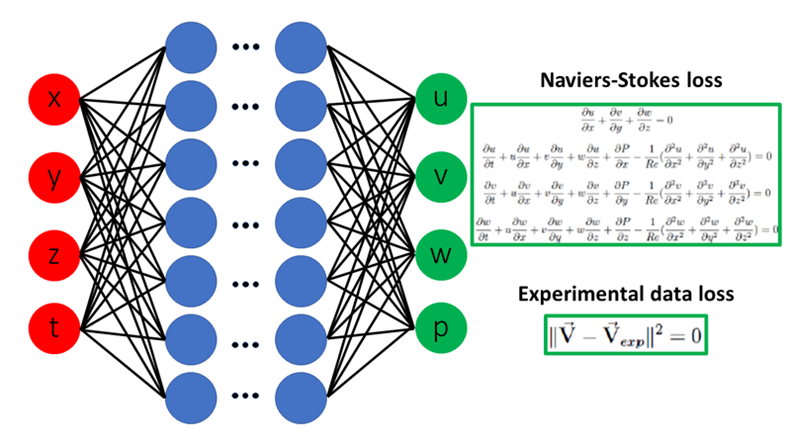
勿論このような課題に対応するために様々な研究がされており、有名なものとしてDeepONet2が挙げられます。DeepONetはまずSの分布を離散化し、ベクトル有限次元のベクトルで表現できるようにします。そして得られたベクトルをPINNsの入力とすることにより、任意のSに対応可能なモデルを構築します
一方で線形な物理現象を対象とする場合、より物理的知識を活かした手法が提案されています。例えばYuankaiらは上式の代わりに、\( u \)に対応するグリーン関数\( G \)と支配方程式 \( N[G] = -\delta \)を学習させます3。任意の\( S \)における\( u \)の解はグリーン関数の重ね合わせで計算できるため、PINNsの結果に対して別途数値計算を施せば、 \( u \) が求まることになります。偏微分方程式とグリーン関数については例えば「物理とグリーン関数4」などを参考にしてください。
ネットワークアーキテクチャに物理的工夫を凝らしたPINNsもいくつか提案されています。例えばAlkhalifahらはヘルムホルツ方程式の解の表現にガボール基底関数が有効であることに着目し、有限個のガボール関数に対する係数を求める方法を提案しました5。なお、ヘルムホルツ方程式の解は各関数を足し合わせることで求まります。このように支配方程式の残差だけでなくアーキテクチャも工夫することは、PINNsの学習を助けることが知られています。
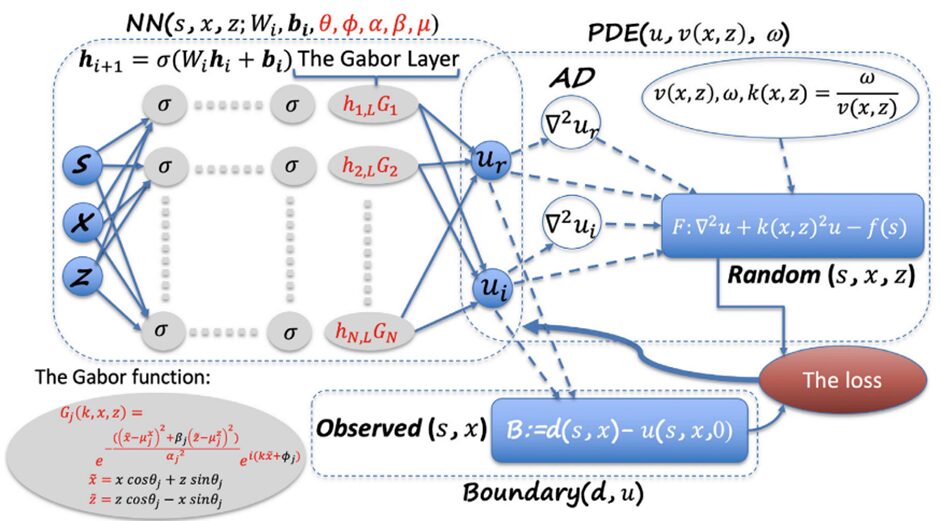
離散化された物理状態における残差の活用
一般的なCAEと同様に時空間を離散化して、その中でPINNsのように残差を活用した学習方法も提案されています。離散化された時空間における残差の計算方法は一般的なCAEと同様で、それゆえCAEの中身についても理解している必要があります。
例えばPhyCRNet6は前時刻の物理状態などを入力として受け取り、次時刻の分布を予測します。これだけを聞くと、一般的なCAEと変わりませんが、PhyCRNetは物理状態を低次元に圧縮し、かつ時間発展をCAEよりも高度なモデルに置き換えることで高速化を図っています。
PhyCRNetの長所として以下の点が挙げられます。
- PINNsと比べて高い精度を達成することが多い
- 離散化された物理状態の扱いについて、CAEの知識を転用しやすい。
一方でいくつか欠点も挙げられます。たとえばPINNsと違って離散化しているため、多数の計算格子や短い時間刻みを要する物理現象に対しては、推論に時間を要することは念頭に入れておくべきでしょう。また、高速化の度合いはネットワークアーキテクチャ(特にレイヤー数)に大きく依存し、場合によってはCAEよりも遅くなってしまうことも注意しなければなりません。
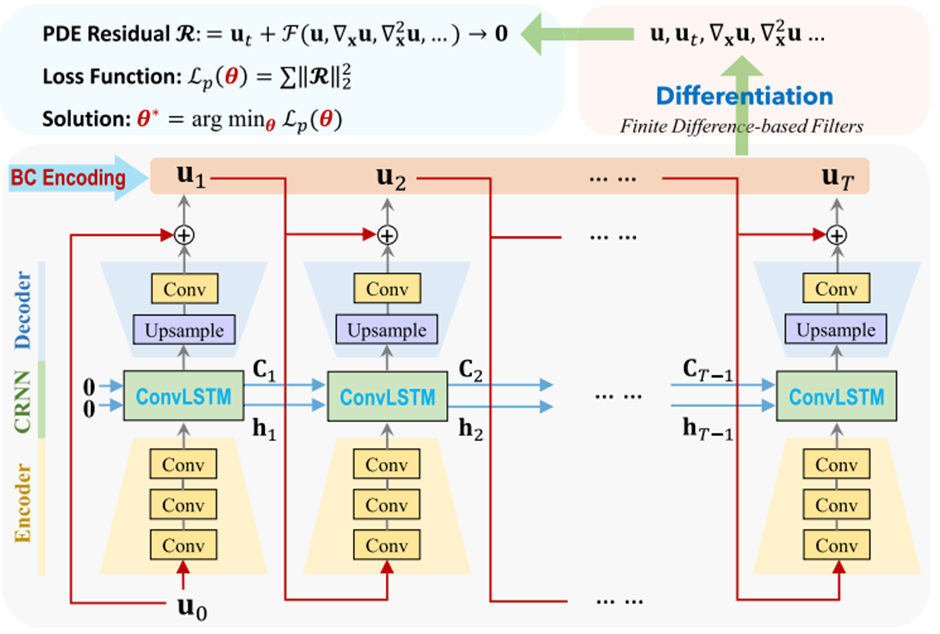
CAE結果の高解像度化
画像解析の分野で深層学習による画像の高解像度化が研究されていますが、同様に低解像度なCAE結果を高解像度化するサロゲートモデルも提案されています。例えばFukami7らは乱流シミュレーションの結果を高解像度化し、単純に多項式補間するよりも良い精度が出ることを紹介しています。このような手法の長所として以下の点が挙げられます。
- 入力が低解像とはいえCAE結果なので、比較的学習が安定する。
- ある微小領域の状態を高解像度化したい場合、近傍の状態を参考にすれば解決することが多いため、ネットワークアーキテクチャがコンパクトに済む。
- 近傍のみに着目している分、高い汎用性のサロゲートモデルが期待できる。
一方で、入力としてCAE結果を用意しなければならないため、サロゲートモデルによる劇的な推論速度向上は見込めません。例えば計算格子数が1/10の低解像CAE結果を用意する場合、サロゲートモデルによる高速化はおよそ10倍となります。しかしながら、10倍高速化するだけでも十分嬉しい事例は多いと思いますので、そういった場合は有効な手法と言えます。
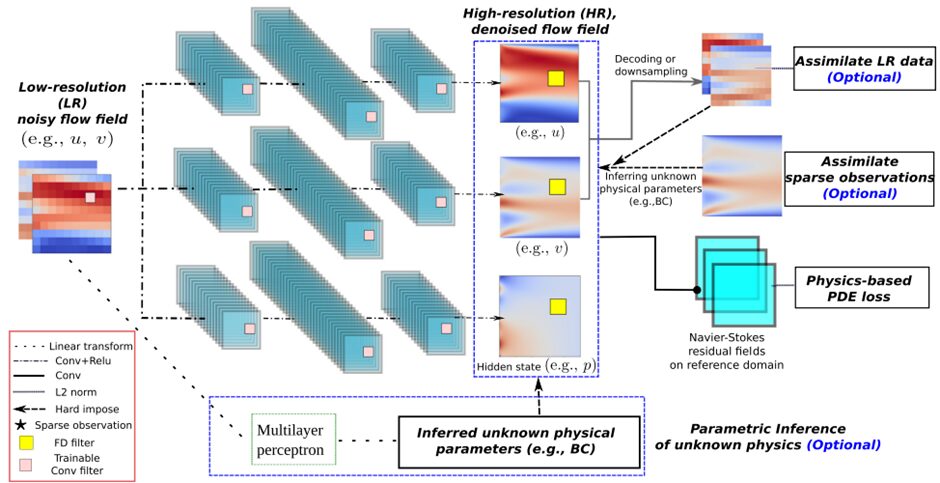
PINNsやPhyCRNetと比べたとき、高解像度化手法の欠点として高解像CAE結果を正解値として用意しなければならないことが挙げられます。そこでGao8らは、支配方程式の残差を誤差関数として利用することで高解像度CAE結果を不要にする手法を提案しました。なお、残差の計算方法はPhyCRNetやCAEと同様です。
CAEの一部アルゴリズムの代替
CAEのアルゴリズムをほとんど残しつつ、計算のボトルネックとなっている部分のみ代替する手法も数多く提案されています。最も活発に研究されているのは恐らく乱流モデルでの利用でしょう。つまり、現時刻の状態から乱流応力を予測するようなサロゲートモデルです。
ところで、そもそも乱流モデル自体が代替的なモデルなため、既存の乱流モデルにより求められた乱流応力を正解値にしてサロゲートモデルを学習しても、結果はよくて既存モデルのコピーとなります。そのため、乱流モデルを一から作るには、DNS(Direct Numerical Simulation)のような乱流モデルを用いない結果から学習する必要があります。
ただし、DNSから乱流応力を出力することはできないため、このときのサロゲートモデルは強化学習のような方法で学習する必要があります。つまり、サロゲートモデルで乱流応力を予測し、それを作用させたときの場の状態を導出します。これとDNS結果との差分を損失とし、サロゲートモデルを学習します。本モデルの長所として以下の点が挙げられます。
- 学習がCAE全体のごく一部であるため、他手法と比較して少ないデータで済むことが期待できる。
- 汎用性の高さ
一方で、推論のほとんどの部分を従来のCAEのアルゴリズムが担うため、劇的な高速化は期待できません。
近年は、サロゲートモデル以外のCAEの箇所も微分可能な形式にする研究も活発に行われています。例えばShankar9らは、FeniCSというFEMソルバーを用い、内装されているアジョイント法の機能を利用することで、CAEの微分可能化を実現させました。アジョイント法自体はトポロジー最適化やデータ同化の分野で昔から使われていましたが、これがサロゲートモデルの学習にどのような影響を与えるかは、今後の研究で解明されていくでしょう。
連続体における内力のサロゲートモデル化に対して、ネットワークアーキテクチャに工夫を凝らす研究もあります。例えばPrantl10らは、学習結果が作用反作用の法則を必ず満たすように、連続畳み込みニューラルネットワークのカーネルを非対称とする方法を提案しました。そして粒子法における内力をサロゲートモデルで代替し、アーキテクチャに工夫を凝らすことの有効性を示しています。また、学習データにはなかったような空間形状であっても、本モデルは液体の流れを精度よく予測できることも確認されています。

学習データにないような空間形状、および異なる粒子数においても良く予測できていることを表している。
さいごに
如何でしたでしょうか。このように物理を加味したサロゲートモデルには様々な種類がございます。また、物理を存分に活用するためには、いずれも高度な物理の知識も必要であることが伝わったかと思います。アイクリスタルは単なるAIの会社ではなく、物理や工学に詳しい社員が多く在籍しております。そんな私達だからこそ提案できるサロゲートモデルで、皆様の製造課題を共に解決できれば幸いです。
アイクリスタルはプロセスインフォマティクスのプロフェッショナル集団です。
当社の技術やソリューションに関心をお持ちの方は、ぜひ当社のホームページで詳細をご確認ください。製造業におけるPIの最適なパートナーとして、皆様のご期待に応えます。
お問い合わせはこちら:お問い合わせフォーム
お気軽にご連絡ください。
参考文献
- M. Raissi, P. Perdikaris, G.E. Karniadakis,Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations,Journal of Computational Physics,Volume 378,2019,Pages 686-707,ISSN 0021-9991 ↩︎
- Lu, L., Jin, P., Pang, G. et al. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat Mach Intell 3, 218–229 (2021). ↩︎
- T. Yuankai, Z. Xiaoping, W. Zhu, J. Lili, Learning Green’s Functions of Linear Reaction-Diffusion Equations with Application to Fast Numerical Solver, Proceedings of Mathematical and Scientific Machine Learning, 2022 ↩︎
- 今井勤、物理とグリーン関数、岩波書店、2016 ↩︎
- T. Alkhalifah, X. Huang, Physics-informed neural wavefields with Gabor basis functions, Neural Networks, 2024 ↩︎
- Pu Ren, Chengping Rao, Yang Liu, Jian-Xun Wang, Hao Sun, PhyCRNet: Physics-informed convolutional-recurrent network for solving spatiotemporal PDEs,Computer Methods in Applied Mechanics and Engineering,Volume 389,2022 ↩︎
- Fukami, K., Fukagata, K. & Taira, K. Super-resolution analysis via machine learning: a survey for fluid flows. Theor. Comput. Fluid Dyn. 37, 421–444 (2023) ↩︎
- Han Gao, Luning Sun, Jian-Xun Wang; Super-resolution and denoising of fluid flow using physics-informed convolutional neural networks without high-resolution labels. Physics of Fluids 1 July 2021 ↩︎
- V. Shankar, R. Maulik, V. Viswanathan, Differentiable Turbulence II, arXiv, 2023 ↩︎
- L. Prantl, B. Ummenhofer, V. Koltun, N. Thuerey, Guaranteed Conservation of Momentum for Learning Particle-based Fluid Dynamics, NeurIPS, 2022 ↩︎