半導体の計測手法を網羅的に解説-結晶構造、キャリア物性から熱物性まで

本稿は、半導体に用いられる計測手法を網羅的に解説した前編です。複数の計測手法を組み合わせて知見を得るマルチモーダル分析について実例を紹介した後編もありますのでぜひご覧ください。

製造プロセスを高度化し、より良いものづくりを実現するためには、まず適切に「測る」ことが出発点となります。半導体の計測・物性評価は、デバイス性能を左右する欠陥（空孔・格子間原子などの固有欠陥、ドーパント、不純物、複合欠陥）を可視化し制御するための出発点です。欠陥は害（非放射再結合・トラップによる劣化）にも益（自由キャリアの供給、キャリアライフタイムの制御、酸素析出物は重金属のゲッタリングシンク）にもなり得るため、SiやGaAsのような従来材料でも、SiC・GaNや2D材料のような新材料でも、成り立ちと振る舞いを読み解くことがより良い半導体デバイスの研究開発に不可欠です^[0-1]。

測定したデータは、適切な解析があってはじめて価値になります。インフォマティクス技術(機械学習などの情報科学を基盤とした技術)では、人手では解析や認識が容易ではない高次元データや複数の形式(モーダル)のデータから潜在構造や非線形相関を抽出できます。これにより、単一の測定では捉えきれない情報を相補的に明らかにできます。また、装置の高スループット化・その場計測の進展により計測データが爆発的に増加する中で、人手での解析のみでは研究開発のボトルネックになる場合もありますが、インフォマティクス技術により解析の再現性とスループットを向上できます。例えば、(1) 複数の測定手法(X線回折やフォトルミネッセンス、二次イオン質量分析法)など異種データの統合解析(マルチモーダル分析)で因果に迫る、(2) 機械学習を用いてパターン認識・異常検知を自動化する、(3) 実験計画や装置条件をベイズ最適化で適応的に更新し自動化する――などで計測や解析に貢献します。実際、XRDでは機械学習を組み込んだ自律測定や位相同定の高速化が実証されています^[0-2]。また、オペランド分光法などで測定される大量のその場観察スペクトルデータを機械学習で高速に解析する手法も開発されています^[0-3]。(オペランド分光法とは，物質・材料・デバイスの反応や機能が進行中の動的な状態を直接その場観測することです。in-situ と比較して，オペランド分析では，適切な環境においた上でさらに積極的に試料に外場を与え，動的過程を観測することによって試料のデバイスとしての機能・反応・劣化のメカニズムを明らかにするという意味が込められています。^{[0-4, 0-5]})

以上を踏まえ、本稿では半導体の主要な計測手法を可能な限り網羅的に整理し、何を測れるかを起点に解説します。これらの章は、これから半導体の計測手法を勉強する方の参考や測定手法を調べる際の入口としてご活用ください。個別の測定手法についての解説は様々な論文や記事がありますが、それにたどり着くためには手法の名称を知らないと検索できないため、まず概要を知っていただくための網羅的に記載されている記事を書くことにしました。できるだけ多くの測定手法に触れるため、各手法の説明は短いですが、より詳しい原理や実際の測定例については、参考文献をご覧いただくか必要に応じてご自身でも調べていただければと思います。筆者は半導体のキャリア物性、光物性および熱物性の評価の経験が多いため、4から6章をより詳しく解説します。4章以降、詳しい解説は折りたたんでおりますので、興味のある方はクリックしてご覧ください。

本稿の後編となる記事では、マルチモーダル分析によるデータ融合によって得られる追加価値について実例を紹介します。計測手法を組み合わせて解析して新たな知見を得るマルチモーダル分析の例が知りたい方は後編をご覧ください。

結晶秩序と対称性（相・配向・テクスチャ）
格子パラメータと歪み状態（格子定数、緩和度、モザイク性）
欠陥とその応力場（転位・積層欠陥など）

XRD／GI-XRD、RHEED、EBSD, ラマン分光

何を測定できるか
格子定数、歪み

化合物半導体では、組成比によって格子定数が変化するため、格子定数から製膜した材料の組成を推測することもあります。
量子井戸などの多層構造を製膜した場合には、スペクトルの形状から各層の膜厚を推測できる場合があり、簡易的な測定として使用されることがあります。

原理

• ブラッグ条件に基づき、ピーク位置から面間隔と格子定数を推定します。ピーク幅・形状から結晶サイズや微小歪みを推定します。
• RSM（逆空間マッピング）は、回折点近傍で試料傾きと検出角を走査し、二次元の強度マップを作る取得モードです。マップの縦方向が面外情報、横方向が面内情報に対応すると考えると直感的にわかりやすく、薄膜の面外・面内格子定数や歪み／緩和を同時に読み分けられます。一次元のθ–2θだけでは重なって見えるピークも、RSMでは位置と形の違いで分離・解釈しやすくなります。^[1-3]
• GI-XRDは浅い入射角で情報深さを表層に限定し、基板からの寄与を抑えて薄膜・表層を特異的に測定する手法です。

何を測定できるか
結晶内の欠陥(転位・積層欠陥・滑り線など)や歪みの分布を2次元マッピングとして広い視野で可視化できます。
ウェーハ広域の欠陥評価に有効です。

原理
欠陥や応力場により局所的にブラッグ条件がずれ、回折強度にコントラストが生じます。反射・透過の各配置で回折像を撮像し、明暗パターン＝欠陥・応力場の空間分布として測定できます。

何を測定できるか
主にMBE(分子線エピタキシー)での結晶成長中にその場観察する際に使われる装置で、成長中の結晶の表面構造を計測できます。

原理
斜入射の高エネルギー電子を用いた表面敏感な回折法です。入射角度が浅いため電子線は試料表面から数原子層しか進入せず、表面層からの回折が得られます。平坦表面ではストリーク状、三次元島状ではスポット状など、像のパターンが表面構造に対応します。

何を測定できるか
結晶性試料の方位解析
多結晶材料の各粒界の面方位、結晶粒径
結晶粒マップや粒径分布

原理
試料に傾斜した電子線を照射すると、試料表面付近の領域の各結晶面で回折電子線が得られます。この後方電子回折から方位や粒径の情報が得られます。

何を測定できるか
応力、結晶性、歪み、温度(熱伝導率)

原理
光を物質に照射すると、光が物質と相互作用することで入射光と異なる波長を持つラマン散乱光と呼ばれる光がでてきます。その波長差は、物質が持つ分子振動のエネルギー分に相当するため、分子構造の異なる物質では、異なる波長を持ったラマン散乱光が得られます。ピーク位置からは化学結合の情報、スペクトル全体の波形から分子構造の情報や結晶構造の違い、ピーク半値幅からは結晶性の違い、ピーク位置のシフトから応力や歪みなど、様々な情報が得られます。ラマン散乱光を用いて、応力、温度、電気特性、配向・結晶性などの様々な状態を調べられます。(文献1-10の図がわかりやすいです。)

装置によってはマッピング測定も可能なため、応力や歪み分布等を測定できます。
ラマン分光を用いて熱伝導率を計測することもできます。^{[1-11, 1-12]}

ラマン分光測定は後述するフォトルミネッセンス測定と近い装置構成のため、4章で説明するフォトルミネッセンスとラマン分光を切り替えて測定できる装置が販売されています。

表面トポグラフィ（粗さ・段差・テラス・パターン形状）の定量、
欠陥の形状・分布（ピット、パーティクル、クラック、粒界など）の把握、
界面・近表面構造（薄膜/基板界面の連続性、層境界の連結性、再構成）の評価

何を測定できるか
表面の三次元高さマップと粗さをÅ〜nmの精度で定量できます。

原理
探針を表面近傍で走査し、探針–試料間力の変化をカンチレバーのたわみや共振応答として検出し、高さ情報に変換します。

原理
導電性探針を表面にサブnmまで近づけ、探針–試料間のトンネル電流を保持するように高さ（Z）を制御します。Z信号が原子スケールの凹凸を反映し、画像化されます。

STMの探針は、とても鋭利で頑丈な金属であることが求められます。試料表面に孤立した原子分子を観たい場合はタングステンに電解研磨法で探針を作成します^{[2-4, 2-5]}。対象によっては白金とイリジウムの合金の針金をニッパーで切断しただけの探針でも測定できる場合があります^[2-5]。

AFMとSTMの違い

AFMは主に形状を測定し、STMでは電子状態や構造を測定します。

AFMは非導電性材料にも対応できるため、試料を選ばず広範な分野で利用されますが、STMでは導電性がない試料を測定できません。

何を測定できるか
数nm級の分解能で広い視野の表面形状・欠陥を迅速に観察できます。
断面観察で界面形状も把握でき、断面SEMを基板上の薄膜の膜厚測定に用いる場合もあります。
後述のEDX/EDSで組成分析も可能です。

原理
集束電子線を走査し、表面から放出される二次電子・反射電子を検出して形態コントラストを得ます。情報深さは主に数nm〜数十nmです。試料は導電性が必要であり、導電性のない試料を測定する場合は、スパッタや蒸着で試料表面を金属で薄く一様に覆います。

断面SEMを行う場合は、断面を観察するために試料をへき開するなどして加工し、断面観察用のステージ等を用いる必要があります。

原理
加速電子（数百 keV）を薄片試料に透過させ、透過・散乱電子の位相/強度の違いを像・回折として検出します。

• TEM/HRTEM：対物レンズで透過電子を結像し、回折・位相コントラストから原子配列や格子縞を得ます。
• STEM：電子プローブを走査し、HAADF（高角度散乱）などの検出器で原子番号依存コントラストを取得します。

TEM観察は超薄片（~<100 nm）への試料作製が前提で、破壊的前処理を行う必要があります。

何を測定できるか
非接触で表面の三次元形状（高さマップ）や欠陥・段差を取得できます。ステップ高さ・テラス・パターン形状、パーティクルやピットなどの欠陥の高さ・体積を評価できます。視野はAFMより広く、μm〜mmスケールのエリアを連続スキャンできます。高さ分解能はサブnmです。

原理

• レーザー走査型共焦点では、対物レンズの焦点面と共役な位置にピンホールを置き、焦点面の光だけを検出器に通します。XYを走査しながらZ（焦点位置）を変えることで、焦点の合った層のみを薄く切り出した光学断層像を積層し、三次元の高さ情報として再構成します。
• 端的に(乱暴に)言うと、共焦点とピンホールにより焦点が合っている場所の光しか検出器に入らないようにしてあり、焦点が試料表面に合うときれいに見える(光が検出器に多く入ってくる)ので、強度が高い位置を試料の高さだと思えば試料の表面の凹凸形状がわかります。

化学組成（主成分・不純物・残渣）の把握、
ドーパント濃度と深さ分布（注入プロファイル、活性化・脱活性、界面での混合）
拡散挙動（拡散長・係数、グレーディング、熱処理による再分布）

SIMS、EDX/EDS、RBS

何を測定できるか
試料中のドーパントや不純物の濃度の深さ方向分布
イメージングSIMS／ToF-SIMSでは面内分布（〜100 nm級まで）も測定可能

原理
一次イオンを試料に照射して表面をスパッタし、飛び出した二次イオンを質量分析して元素・同位体情報を得ます。スパッタ時間を深さに換算してプロファイル化します。元素やマトリクスによりイオン化確率が変わるため、マトリクス効果を補正するために標準試料や内部標準を併用します^[3-3]。試料の元素を飛び出させる測定のため、破壊的測定です。

何を測定できるか
SEM(走査型電子顕微鏡)やTEM(透過型電子顕微鏡)の観察範囲そのままに元素種と相対濃度の面内マップをナノ〜サブμm分解能で取得できます。質量%(wt%)や原子%(at%)で原子の割合を測定可能です。標準試料による定量化をしていない場合は半定量分析と言われます。

原理
電子線照射で生じる特性X線のエネルギーを検出し、元素を同定・定量します。空間分解能はSEMで数十 nm〜サブμm、TEMでナノスケールです。EDXやEDS自体は非破壊測定ですが、SEMやTEM観察用に試料を加工する場合は破壊的測定になります。

何を測定できるか
元素組成と面密度（膜厚）を標準無しで非破壊に絶対定量できます。

原理
MeV級の軽イオン（Heなど）を照射し、ラザフォード散乱によって後方に散乱されるイオンのエネルギーから散乱相手の元素と深さを推定します。衝突した相手の原子核が He イオンに比べて十分に重ければ、He イオンはほとんどエネルギーを失わずに散乱されます。一方、軽い原子核に衝突した場合には相手の原子核を弾き飛ばして He イオンはそのエネルギーを失うので、散乱後の He イオンは入射時よりも低いエネルギーを持って試料から現れることになります。このため、散乱した He イオンのエネルギーを測定すればどのような質量を持った原子核が試料中に存在するかがわかります。イオンが物質中を単位距離進む時のエネルギー損失は阻止能と呼ばれ、いろいろなイオンと物質の組み合わせに対して半経験式が与えられています。この阻止能を用いて、散乱した He イオンのエネルギーを測定することで、どの深さにどのような元素が存在しているのかを評価できます。

RBS測定は、MeV級のHeイオンを出す小型加速器とビームライン、超高真空チャンバー等が必要なので、設備規模・保守・放射線安全の観点から、測定は大学・研究機関や一部の専門受託機関に限られます。

発光波長、光吸収係数、バンドギャップ、欠陥準位

定常PL、EL、CL、FT-IR、フォトリフレクタンス、 DLTS

何を測定できるか
発光波長（バンドギャップ、欠陥準位由来の発光）、発光強度（結晶品質、欠陥密度の指標）

原理
励起光により生成した電子・正孔が再結合する際の発光スペクトルを測定します。ピーク位置(発光波長=発光エネルギー)はバンドギャップや欠陥準位に対応し、ピーク強度や幅は再結合経路や結晶性を反映します。直接遷移型半導体では強い発光が得られますが、Siのような間接遷移型半導体でも適切な測定系では測定可能です。
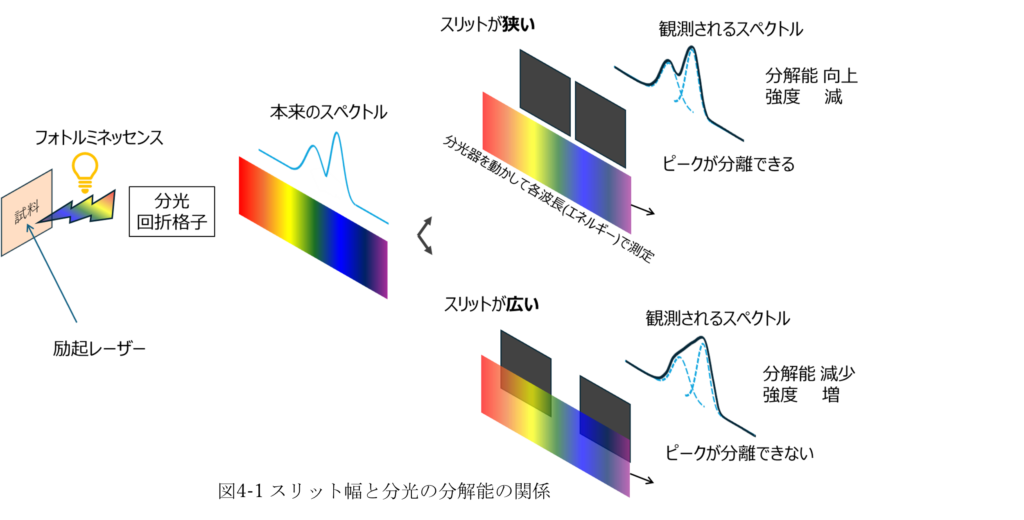
試料に電子正孔対を生成する必要があるため、バンドギャップよりも高いエネルギーの波長のレーザーを用意する必要があります。また、試料の発光波長に応じた分光器、回折格子および検出器が必要です。励起光の波長と光吸収係数( 1/光侵入長)の関係性から、励起光の波長によって試料のどの厚みまでを測定しているかに注意して解析する必要があります。

測定に際し注意すべき点はこちらをクリックしていただくとご覧いただけます。

試料から生じたわずかな光を検出したいので、照明を消し、窓から太陽光が入らないようにして測定を行います。検出器は試料から出るわずかな光を検出できるよう高感度ですが、実験室の照明や太陽光が検出器に入ると故障の原因になり得るため、検出器を起動している際は照明をつけないように気を付ける必要があります。また、パソコンのディスプレイからの光や装置のボタンなどについているLEDの光などが迷光として検出器に入らないように注意しないと試料からの発光ではないピークが検出される可能性があります。

分光器の長さ と 分光器のスリットの幅がスペクトルの波長分解能と信号強度に関係します。図4-1に示しています。
・分光器長さ : 長いほど波長分解能が上がり、信号強度は下がります。
分光器長さが長いほど細かく分光できるので分解能は向上しますが、検出器に入る光量は減ってしまいます。

・スリット幅 : 狭いほど波長分解能が上がり、信号強度は下がります。
スリット幅が狭い方が、分光した光をより細かく分けて検出器に入れるため分解能は向上しますが、検出器に入る光量が減るので強度が下がります。
測定の際には、スリットの幅は測定可能な強度が出る範囲内で狭くするのが良いです。波長分解能が上がることで、重なっていたピークが分離された状態で測定できるようになる場合や、潰れたガウス分布のような不適切な形状で測定されたピークが適切な形状で測定できるようになる可能性があります。逆にスリット幅が広すぎる、励起光強度が強すぎる等で、試料からの発光が強すぎると検出器の信号が飽和してしまい、不適切なつぶれたピークとして観測してしまう場合があります。

類似の手法である多光子励起PL、近接場光PL、エレクトロルミネッセンス、カソードルミネッセンスについての説明はこちらをクリックしていただくとご覧いただけます。

多光子励起PL^[4-4]

通常のPLでは半導体が光吸収できるバンドギャップ以上のエネルギーを持った励起光を照射して測定を行いますが、多光子励起PLは違います。バンドギャップ以下の波長の光でも、フェムト秒レーザーを用いて短時間に集光して狭い範囲に照射すると、2光子分のエネルギーまたは3光子分のエネルギーを使ってバンドギャップ以下の波長の光でも励起できます。集光させる位置は光学系を使って、集光レンズやミラー等で制御でき、基本的にはバンドギャップ以下の波長の光は吸収されないため、試料内部を3次元的に計測可能です。一般に、欠陥ではフォトルミネッセンス発光強度は低下するため内部の欠陥の形状を非破壊で3次元的に観測可能です。

近接場光PL^[4-5]

近接場光は、光が全反射する際に界面から外側へ“にじみ出す”ように生じる光です^[4-6]。通常の光はレンズなどを用いても回折限界(波長/2程度)より小さく集光することはできませんが、近接場光は、光が界面から「にじみ出る」時にできる局所的な場なので、レンズでは不可能な“波長未満のスポット”を作れます。近接場光PLでは、その近接場光を励起に使うことで、とても高い空間分解能でのPL測定が可能になります。

PLに類似の手法 ELとCL

EL(エレクトロルミネッセンス) ^[4-7]
類似の手法としてエレクトロルミネッセンス(EL)がありますが、電極形成が必要です。主にデバイス構造ができて電極形成された後に行われます。PLはデバイス構造ができる前にまず光るか、結晶性に問題がないかなどを電極なしに確認できます(発光強度が大きいほど結晶性が良いと一般に言われています)。

CL(カソードルミネッセンス) ^[4-8]

加速した電子を試料に照射した際に生じる発光を検出する手法をカソードルミネッセンス(CL)と言います。加速電子はSEMでも用いられるように数nmに絞ることができるため、高い分解能で微小領域を測定することができます。

PL、ELおよびCLは、発光する過程自体は同じですが、励起する方法が違います。PLでは励起光の光吸収した領域(試料の光吸収係数と励起光の波長による)とキャリアの拡散長の範囲内での発光が検出されます。ELでは電子を注入した場所からの発光になります。また、CLでは電子の加速電圧に応じて侵入深さが変わり、電子が侵入した範囲からの発光になります。

何を測定できるか
光吸収係数、局在振動モード、不純物や格子欠陥に関連する吸収ピーク

原理
赤外光を照射し、試料の透過または試料からの反射スペクトルをフーリエ変換して得ます。透過していない光は試料に吸収されていることから光吸収係数を測定できます。また、吸収端からバンドギャップを推定できます。(吸収スペクトルからバンドギャップを算出するのは大雑把だという意見もあります。筆者もそう思います。) また、原子や欠陥由来の局在振動モード（LO/TO phononや水素結合由来ピークなど）が現れるため、欠陥や不純物の同定が可能です。Siや化合物半導体における酸素・炭素・水素関連の局在モード評価に多用されます。Siでは酸素濃度の定量に用いられます。

何を測定できるか
バンドギャップ

原理
試料に変調光を照射してキャリアや電場を周期的に変化させ、その状態での反射率変化を測定します。定常PLに比べて非発光の材料にも適用でき、バンドギャップやサブバンドギャップ遷移を高精度に決定できます。

PR測定では、光を照射することで表面電場が変調され、それにより反射率 R が微小に変化します。検出される量は通常、ΔR/Rです。
この変化は複素誘電関数 ε(E)=ε₁(E)+iε₂(E) の変調に起因しており、吸収端や臨界点（バンドギャップや遷移エネルギー付近）で顕著な信号が現れます。
ただし PR で直接測定できるのは「反射率変調の実部寄与」が主体であり、ΔR/Rの信号そのままではバンドギャップの評価が難しいです。そこで、クラマース–クローニッヒ(KK)変換を行います。^[4-10]

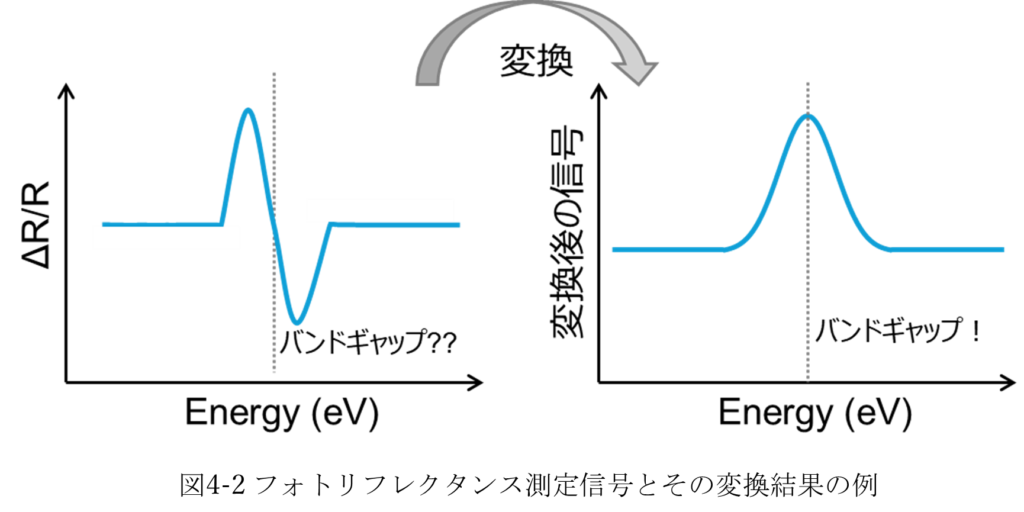
KK変換は、複素関数の実部と虚部を結びつける関係式で、実部の情報から虚部の情報を得られます。変換後のスペクトルのピークエネルギーからバンドギャップを同定できます。(KK変換前のΔR/Rのスペクトルはピーク位置を同定することが容易ではないスペクトル形状になっていることが多いですが、KK変換後は、ピークを同定しやすいスペクトル形状になっているはずです。図4-2にその概要を示します。)

何を測定できるか
欠陥準位のエネルギー位置、捕獲断面積、欠陥密度

原理
試料にパルス的にバイアスを印加してキャリアをトラップに捕獲させ、その後の放出電流の時間応答を測定します。温度依存測定を行うことでトラップの活性化エネルギーと捕獲断面積を決定可能です。光学手法では直接見えにくい深在準位を定量化できるため、電子デバイスの信頼性評価に必須です。
試料に電極を形成して測定します。基本的にはショットキーの電極を形成する必要があります。

キャリア濃度・移動度、寿命、再結合経路の定量化

Hall効果測定、タイムオブフライト、SPV、時間分解PL、μ-PCD, TR-FCA

何を測定できるか
キャリア(電子または正孔)濃度 と移動度 、電気伝導率( \( \sigma = n \times \mu \) )

原理
電流を流した試料に磁場を直交させると、ローレンツ力でキャリアが横方向に偏りホール電圧が発生します。電圧から ホール係数  を求め、  や   を算出します。

Hall測定はVan der Pauw法という手法で行われます^[5-2]。
測定には4点のオーミック電極が必要で、その配置や大きさはVan der Pauw法を理解して試料準備を行う必要があります。

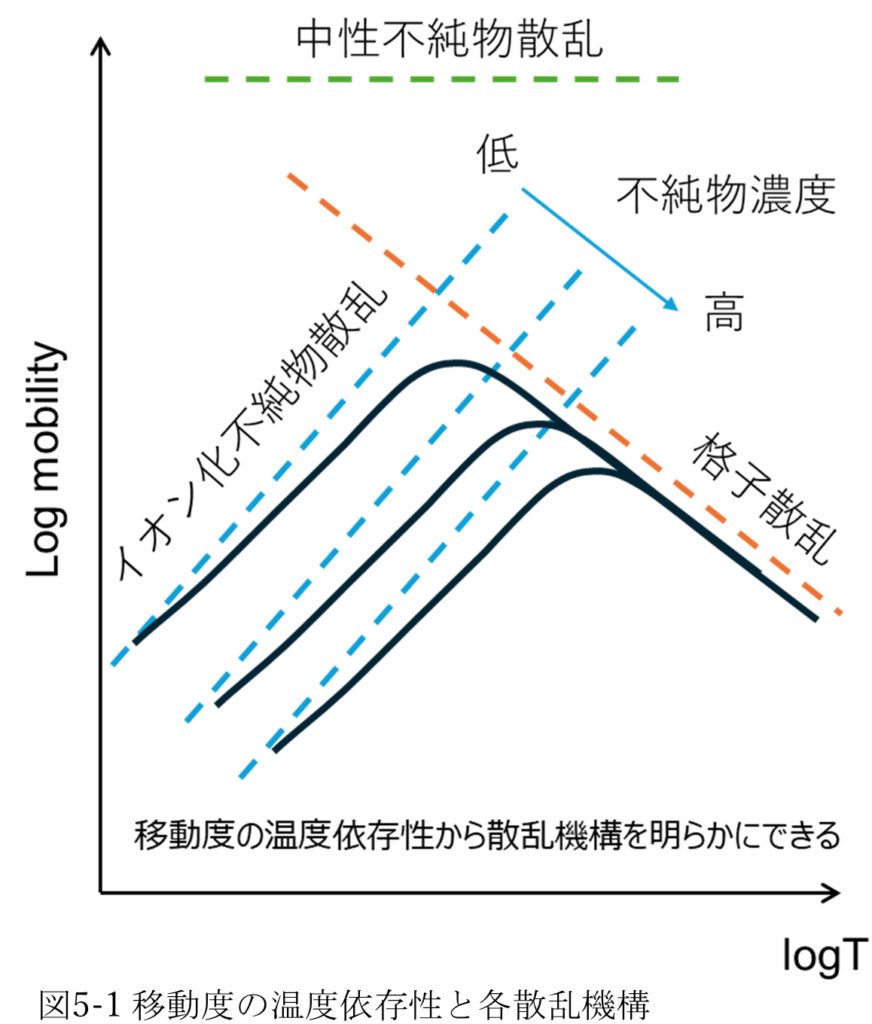
オーミック電極を得るには、測定したい材料に対して適切な金属を選択することと、電極の作成方法(蒸着、スパッタなど)やアニールを行う場合はアニール温度や時間を適切に設定する必要があります。 移動度の温度依存性を測定することで移動度の散乱機構を評価できます^[5-7]。散乱機構^[5-3,4,5,6]には、格子散乱^[5-3,4,5]、イオン化不純物散乱^[5-3,4,5]、中性不純物散乱^[12]、キャリア間散乱^[5-7,5-8]などがあり、図5-1に示すようにそれぞれ温度による変化が異なるため散乱機構を評価できます。
温度が変化しても電極がオーミック特性を維持しているか確認する必要があります。

Hall測定において、導電率が低い(抵抗率が高い)ために測定できない場合の対処法である光を照射しながらHall測定した場合の解析手法の注意点や、多数キャリアと少数キャリアの濃度差が小さい場合の測定についてはこちらをクリックしていただくとご覧いただけます。

電気伝導率が低い(キャリア濃度が低い)材料を測定するのは難しい場合がありますが、その際は光を照射しながら測定することで、光励起によりキャリアが生じ、測定が可能になる場合があります。
まず、光を照射しない暗中での測定について式を使って説明し、その後、光照射時のHall測定結果の解析に用いる式を説明します。

光照射しない暗中の場合(一般的な測定)

光を照射しない暗中での導電率 とホール係数 は以下の通りです (Hall測定では導電率とHall係数が測定されます)。 これらは、測定中に印可した電圧や磁場によるローレンツ力から算出されます。

\[ \sigma = q(n \mu_e + p \mu_h) \]

\[ R_H = \frac{p {\mu_h}^2 – n {\mu_e}^2}{q(n \mu_e + p \mu_h)^2} \]

ここで、\( q \):素電荷、\( n \):電子濃度、\( p \):正孔濃度、\( \mu_e \):電子移動度、\( \mu_h \):正孔移動度です。例えば、p型半導体で、\(n\)が\(p\)よりも何桁も小さい場合は、\(n\)がついている項を無視でき、以下の式になります。

\[ \sigma_h \approx qp \mu_h \]

\[ {R_H}^h \approx \frac{p {\mu_h}^2}{q (p \mu_h)^2} \]

\[ \approx \frac{1}{qp} \]

この2つの式から、\( \mu_h = {R_H}^p \times \sigma_p \)により、正孔移動度を算出できます。n型でpを無視できる場合は、同様の手順でn型半導体中の電子移動度を測定可能です。このためHall測定は多数キャリアの移動度を測定できるといわれています。

しかし、近似が成り立たない、\( n \)と\( p \)の差が小さく、一方を無視できないような場合は注意が必要です。例えば、わずかにp型だが、\( n \)と\( p \)が近い値の時、\( R_H \)の分子は\( p {\mu_h}^2 – n {\mu_e}^2 \)のため、\( n \)が\( p \)に近いほど\( R_H \)は０に近い値になります。すると、\( \mu_{hall} = R_H \times \sigma \)で求めた移動度は何の移動度でしょうか？これは電子移動度でも正孔移動度でもない値だと筆者は考えています。
以上のことから、筆者はHall測定で測定された移動度はHall移動度と書き、正孔移動度を”ホール移動度”とは書かないようにしています。

このため、n型かp型かが曖昧で、キャリア濃度が不明な資料に対して測定されたHall移動度を電子や正孔の移動度とするのは避けるべきだと思います。\( R_H \)が正なら\( p \)型、負なら\( n \)型と判定されますが、それについても、\( R_H \)の式の分子から、\( \mu_h \)に対して\( \mu_e \)がとても大きな値であればp>nであっても負の数になりえるため測定する対象によっては注意が必要です。

光照射時の測定 (普段は使わない方法)

光を照射すると光励起キャリアが生成されます。光励起キャリア濃度を、電子：\( \Delta n \)、正孔：\( \Delta p \)とします。すると導電率\( \sigma \)と\( R_H \)は、以下のようになります。

\[ \sigma = q((n + \Delta n) \mu_e + (p+ \Delta p) \mu_h ) \]

\[ R_H = \frac{(p+ \Delta p) {\mu_h}^2 – (n + \Delta n) {\mu_e}^2}{q((n + \Delta n) \mu_e + (p+ \Delta p) \mu_h )^2} \]

光照射によってキャリア濃度が増えることで導電率が上がり、導電率の低い試料に対しても測定できるようになる場合があります。ここでの測定できるとは、導電率が上がって電流が流れるようになるのでHall効果測定を実施可能になるという意味です。

\( \sigma \)と\( R_H \)の式を見てもわかるように、光照射すると測定が実施できるようになるからと言って得られた値が測定したいものだったのか、意味のある量だったのかは確認する必要があります。一般に、\( \mu_e > \mu_h \)のため、光照射しながら測定されるHall係数\( R_H \)は、負の数になる傾向があり、照射する光量を増やして\( \Delta n \)と\( \Delta p \)が大きくなるほど は小さくなる(負の数で絶対値が大きくなる)傾向があります。

また、光照射下ではキャリア移動度(\( \mu_e \):電子移動度 、 \( \mu_h \) :正孔移動度)が変化する可能性があります^{[5-9,10,11,12]}。移動度を測定する目的で強い光を照射しながら測定することは避けた方がよいと考えます。

参考文献5-9の論文では、太陽電池にレンズで集光した強い光を照射した際に変換効率が低下する問題について、移動度の変化が影響しているのではないかという仮説を検証するために光照射下での移動度をHall測定の結果から求めています。n型とp型Siの両方を測定し、得られたn型とp型それぞれの\( \sigma \)と\( R_H \)の4つの式から、\( \mu_e \)と \( \mu_h \)を算出し、光強度が強いと移動度が減少することを示しています。解析方法の詳細や太陽電池に与える影響は参考文献をご覧ください^[5-9,5-10]。

何を測定できるか
ドリフト移動度 μ

原理
薄膜に電圧を与えた状態で、一方の電極付近にパルス光を照射し、生成キャリアが電界で移動して反対電極に到達するまでの電流波形を測ります。波形からキャリアが電極に到達した時間\( t \)を読み、\( \mu = d/(Et) \)（厚さ d、電界 E）を求めます。(文献5-14のアニメーションがわかりやすいです)
(測距の文脈でもタイムオブフライト(TOF)という言葉が使われますが、それはレーザーを照射して反射して戻ってくるまでの時間をもとに距離を測る手法で別物です。)

何を測定できるか
少数キャリア拡散長 L、有効寿命 τ_eff
重金属により再結合中心が形成されると、再結合中心にキャリアが捕獲されるため、キャリアの拡散長が短くなります。このことから、後述のDLTSと組み合わせてp型Si中のFe濃度を測定できます。測定限界は10⁸ cm^-3程度で、高感度です。重金属汚染を確認するためにSiウェーハメーカー等ではSPV法による測定が行われています。

原理
励起光のオン・オフや波長を掃引しながら、透明電極等を用いて表面の仕事関数差（接触電位差）の変化＝表面光電圧を測ります。吸収係数とSPV応答の関係から生成・再結合の広がりを逆算して L を求め、時間応答から τ_effを推定します。かなり低注入(キャリアが少ない条件)での測定が可能です。ライフタイムは注入量で変化する場合がありますが、次の時間分解PLの項で説明します。

何を測定できるか
有効寿命(ライフタイム) τ_eff、再結合係数（A/B/Cの寄与）、外部量子効率 原理
4章で説明したPL測定をある発光波長に対して、励起光を照射してからの時間変化を測定する手法です。光励起で生じた電子・正孔の発光再結合光を計測することはPL測定と同じです。TRPLは励起レーザーのパルス光を光吸収し、生じた電子正孔の発光再結合による発光強度が時間経過により減衰していく曲線(図5-2)から τ_eff を求め、注入密度依存からSRH（A）／発光（B）／オージェ（C）の支配を切り分けます（高注入でC優勢、低注入でA優勢など）。

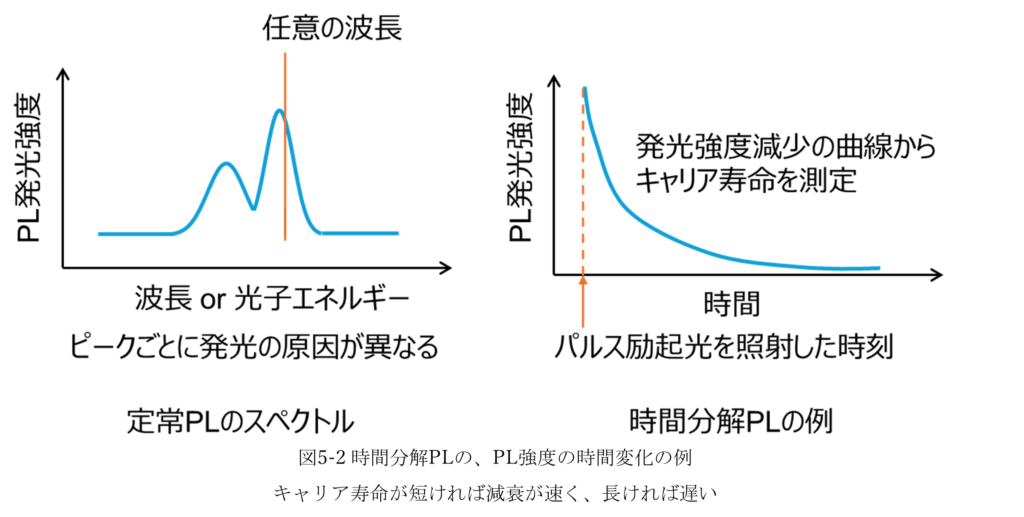
再結合係数とは、以下の式で表される式の係数A, B, Cのことです。

\[ \frac{dn}{dt} = -An-Bn^2 -Cn^3 \]

nは過剰キャリア濃度、tは時間。Aは、SRH(ショックレーリードホール理論による非発光)再結合の係数。SRH再結合は、結晶中のトラップ準位を経由した電子と正孔の再結合です。Bは発光再結合の係数。Cはオージェ再結合の係数。オージェ再結合は高注入条件（励起光強度が高い）で支配的になり、低注入条件では主にSRHと発光再結合が生じます。
つまり、励起光強度によってライフタイムは変化しうるので、励起光強度に注意する必要があります。

測定ではフォトルミネッセンスの発光スペクトルからある発光波長を選んで測定することが多いです。発光には起因となる準位があるので、どの発光波長(エネルギー)でのTRPLを行うかは検討する必要があり、論文等を読む場合も注意する必要があります。

フォトルミネッセンスの信号が得られる(光る)材料でないと測定できません。(主に直接遷移半導体です。間接遷移半導体のSiもフォトルミネッセンス信号は得られるので、結晶性や装置構成によって信号が得られるかどうかが変わると思います。)

何を測定できるか
キャリアの有効寿命(ライフタイム) τ_effを非接触で取得できます。走査して測定することで面内マップを測定可能でウェーハ内の分布を測定できます。

原理
パルス光で過剰キャリアを生成し、その後のマイクロ波反射強度の時間変化を測定します。マイクロ波の反射強度は試料の導電率変化に比例します。そして、導電率は(基本的には)キャリア濃度に比例するため、マイクロ波の反射強度の時間変化の減衰曲線から τ_eff を求めます。走査すれば寿命マップが得られ、表面パッシベーションや金属汚染の影響を可視化できます。

Siウェーハを測定する場合は、表面再結合の影響を除外するため、フッ酸で表面の酸化膜を除去した後、ヨウ素溶液中にSiウェーハを浸けた状態で測定を行います。研究室レベルではジッパー付きの袋にSiの試料片とヨウ素溶液を入れて測定します。

TR-PLでは、フォトルミネッセンス信号が得られないとライフタイムを測定できませんが、μ-PCDでは発光しない材料でも測定できる可能性があります。

一般に、直接遷移半導体のライフタイムはナノ秒程度に短く、間接遷移半導体のライフタイムはマイクロ秒からミリ秒です。TR-PLは発光しやすい直接遷移半導体の計測を行うことが多いので、ナノ秒でも計測できるような装置構成であることが多いと思われます。一方でμ-PCD法は、完成品として販売されている装置では間接遷移半導体であるSiウェーハを測定するための装置構成になっていることが多く、マイクロ秒以上のライフタイムを測定する構成になっていることが多いと思われます。μ-PCD法でも装置構成によってはナノ秒のライフタイムの測定が可能です。

何を測定できるか
有効寿命(ライフタイム)

原理
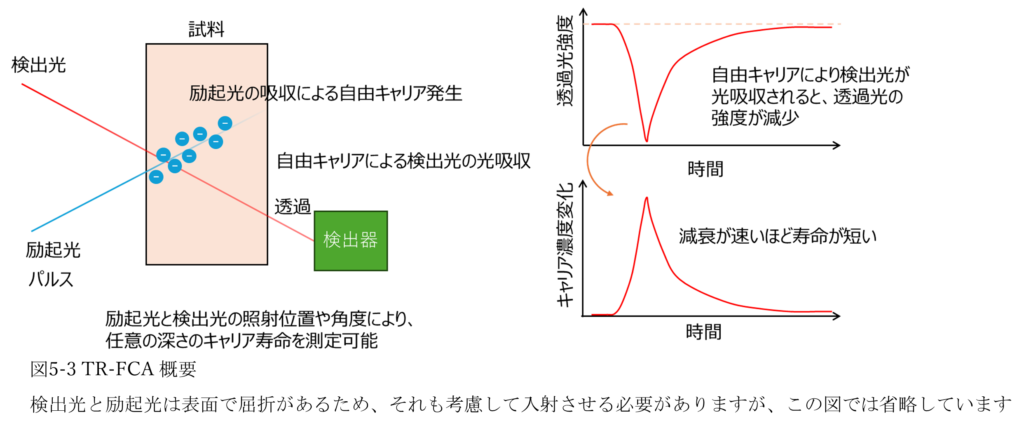
自由キャリアが光吸収することを利用し、透過光の強度変化からライフタイムを測定する手法です。自由キャリアを生じさせる励起光と透過光強度を測定するための検出光の照射する角度をそれぞれ工夫することで図5-3のように任意の深さのキャリア寿命を測定可能です。

透過光を測定するため、両面鏡面の試料を用意する必要があり、励起光は試料が光吸収する波長のレーザーで、検出光は試料を透過する波長のレーザーを用意する必要があります。また自由キャリア吸収は多くのキャリアを励起させて光を吸収させる必要があり、自由キャリアによる光吸収量は少ないためノイズを除去して透過光の微小な変化を適切に検出する必要があります。

熱伝導率・熱拡散率・比熱・界面熱抵抗

測定手法によって、得意とするサイズ(薄膜orバルク)などが異なるため適切な手法を選ぶ必要があります。(バルクとは、大きさが変化しても性質に変化がない程度に大きい材料のことを指しています。対義語かのように薄膜や界面という言葉が使われますが、サイズや表面によって性質が変化する材料を指しています。)

ロックインサーモグラフィ、TDTR、FDTR、レーザーフラッシュ法、3ω法、(2章で説明したラマン分光も熱伝導率測定が可能です)

何を測定できるか
熱伝導率・界面熱抵抗、デバイスの発熱箇所を画像として検出できます

原理
温度変化をサーモグラフィで検出する手法です。ロックインアンプという、ノイズに埋もれた中から特定の周波数をもつ信号を取り出す手法を用いてわずかな温度変化でも検出できるようにしています。ある周波数で電圧印加またはレーザーの照射によって加熱し、加熱と同じ周波数の信号をサーモグラフィで検出します。サーモグラフィなので、画像として測定が可能で、熱伝導率の測定や界面の熱抵抗の測定、半導体デバイスでは電圧の印加による発熱を検出可能で、動作時にどこが何度上昇するかなどを調べることができます。

何を測定できるか
薄膜の熱伝導率・界面熱抵抗

原理
温度変化により反射率が変化することを利用して熱伝導率を測定する手法です。超短パルスレーザーによりポンプ光とプローブ光を用意します。ポンプ光で試料表面を瞬間的に加熱し、プローブ光が照射される遅延時間を変化させながらプローブ光の試料表面からの反射強度を観測します。加熱による温度変化で試料表面の反射率が変化し、プローブ光の反射強度が変化します。測定したプローブ光の反射強度変化から、熱伝導率や界面熱抵抗が求められます。熱伝導率の高低によって、温度の時間変化が異なり、それが反射強度の時間変化に反映されるため、熱伝導率等を測定できます。特に nm〜μm 厚さの薄膜評価に有効です。

試料表面に金属膜を用意して、そこにレーザー光を照射して測定することが多いです。金属は温度変化による反射率の変化が大きく測定しやすいためです。金属の熱伝導率、金属と測定したい材料間の界面熱抵抗、および測定したい材料の熱伝導率を測定することになります。

何を測定できるか
熱伝導率・界面熱抵抗
周波数依存性を利用するため、TDTRよりは広い空間スケールや深さ方向の情報を得られます。
TDTRよりは広いと言っても薄膜の測定が可能であることは変わりません。

原理
連続レーザーを強度変調し、周期的加熱を与えて反射率変化を観測します。変調周波数を変化させることで、熱拡散長(熱浸透深さ)が変化し、深さ方向の熱特性を抽出可能です。変調周波数が低いと熱拡散長が長く、周波数が高いと短いです。薄膜・バルクの両方で測定できます。

熱を加えるためのレーザーと検出するためのレーザーの距離を離して測定することで、異方性のある材料に対しても測定が可能です^[6-5]。

FDTR法を用いて多結晶材料の粒界の界面熱抵抗の2次元マッピングを測定する方法(Gibbs excess approach)もあります^[6-6]。

TDTRとFDTRは、測定したい範囲によって使い分けます。TDTRの方がより熱拡散長が短いので、薄膜や界面の測定に向いており、FDTRは、TDTRよりは広い範囲を測定するのに向いています。装置導入にはTDTR測定装置の方が高価だと思われます。おそらくパルスレーザーが高価なことと、プローブを遅延させる光路を組んで、そこから再びポンプと同じ光路に戻すセットアップに労力がかかるためだと思われます。

電極(加熱用)とサーモリフレクタンス測定を組み合わせて熱伝導率を測定する2ω法もあります^[6-7]。

何を測定できるか
薄膜やナノ構造体の熱伝導率

原理
試料表面に細線電極を配置し、交流電流を流すとジュール加熱が生じます。この発熱は入力周波数の 2倍成分（2ω）を含みます。発熱による温度上昇によって電気抵抗が変化し、電圧に 3倍成分（3ω）が現れます。この 3ω成分の振幅・位相から試料の熱伝導率を解析します。
試料に電極を形成するため、破壊的測定です。

何を測定できるか
バルク材料の熱拡散率

原理
真空チャンバーに入れた試料片の片面をパルスレーザーで瞬時に加熱し、反対面の温度上昇曲線を赤外検出器で測定します。この応答曲線から熱拡散率を解析します。測定できるのは熱拡散率であり、熱伝導率を求めるには比熱と密度の情報が必要です。固体材料の標準的評価法として広く用いられています。
バルク材料の測定に用い、薄膜の測定はできません。レーザーを光吸収しない材料の場合、カーボンスプレーなどを照射して加熱できるようにします。

本稿では、半導体材料の評価に用いられる多様な測定手法を整理し、それぞれで測定できる物理量や特徴を概観しました。測定対象や必要な分解能に応じて手法を使い分けることが重要です。
本稿がこれから計測手法を学ぶ方の理解の一助となれば幸いです。

良いものを作るためには、製造プロセスを高度化し、最適化していくことが不可欠です。その出発点となるのが計測であり、正確な計測によって初めて材料や製品の状態を理解し、改善につなげることができます。本稿で解説した計測手法は、プロセス改善の基盤となるデータを提供し、ものづくりを一段と進化させる鍵となります。

後編では複数の計測手法を組み合わせることで、新たな知見を得るマルチモーダル分析について紹介しております。ぜひご覧ください。

参考文献