多目的ベイズ最適化｜複数の目的を最適化する手法を基礎から実装まで解説

\( \def\bm#1{{\boldsymbol #1}} \)

　ベイズ最適化 (Bayesian Optimization) はマテリアルズ・インフォマティクス (Materials Informatics; MI) の代名詞といえるほど MI における主要な最適化手法として広く知られるようになってきましたが、プロセス・インフォマティクス (Process Informatics; PI) においても重要な最適化手法の一つです。本記事ではベイズ最適化の中でも、製造プロセスにおける「品質特性の最大化とコストの最小化の両立」のように、複数の目的を最適化する多目的ベイズ最適化 (Multi-Objective Bayesian Optimization; MOBO) という手法について、基礎から実装までを一通り解説します。

　実装には様々な方法がありますが、本記事では Python による実装を前提として、その中でも本格派といえる GPyTorch と BoTorch を用いた多目的ベイズ最適化の実装を解説します。

なお、プロセス・インフォマティクスについては次の記事をご覧ください。
【プロセスインフォマティクス入門】製造プロセス最適化のための情報技術を易しく解説

　本記事はかなり専門的な内容を含んでいるため、中級～上級といったレベル感になっています。想定読者はベイズ最適化や多目的最適化に興味がある人、それらを使って製造プロセスを最適化したい人、特に技術者です。しかし、簡単に目を通すだけでも多目的ベイズ最適化の基礎や実装のイメージが掴める内容になっていますので、是非ご一読ください。

　本章では、多目的ベイズ最適化を理解するための前提となるベイズ最適化について説明します。

　ベイズ最適化 (Bayesian Optimization) は、ブラックボックス関数（関数の具体的な形が分からない、あるいは解析的に扱いづらい関数）の最適解を効率的に探索するための最適化手法です。確率モデルに基づいた効率的な探索によって最適解を得るのに必要な試行回数を減らすことができるため、特に、一回の試行に大きなコスト（時間・費用・人手など）のかかる実験やシミュレーションに対して威力を発揮します。

　ベイズ最適化の主な要素は、目的関数の未知の関数形をモデル化する代理モデルと、次に評価すべき最も有望な点（試行条件）を決定するための獲得関数 (Acquisition Function) です。代理モデルとしては、予測値とその不確実性の両方を出力できるガウス過程回帰 (Gaussian Process Regression; GPR) が一般によく用いられます。

　ベイズ最適化は、機械学習におけるハイパーパラメータの最適化や、MI における物質探索の手法などとして活用され広く知られるようになりました。

　ガウス過程 (Gaussian Process; GP) は任意の有限個の点における関数値が多変量正規分布に従う確率過程です。ガウス過程回帰 (Gaussian Process Regression; GPR) は、このガウス過程を事前分布として用いて、観測データを条件として未知関数の事後分布を推定するベイズ的回帰手法です。したがって、点推定ではなく「入力に対して出力がどのような確率分布に従うか」を予測します。

　ガウス過程を一意に決定するには、平均関数 \( m(\bm{x}) \) と共分散関数 \( k(\bm{x}, \bm{x}’) \) を定義します。共分散関数は「カーネル関数」とも呼ばれ、その値は二つの入力 \( \bm{x} \) と \( \bm{x}’ \) に対応する関数値の相関（類似度）を表します。カーネルの選択は GPR の柔軟性や表現力を左右し、RBF (Radial Basis Function) カーネルや Matérn カーネルなど多くのバリエーションがあります。

　実際の観測では、例えば真の関数値 \( f(\bm{x}) \) に観測ノイズ \( \varepsilon \) が加わった値が得られるとします。

\[ y = f(\bm{x}) + \varepsilon \]

ここで、観測ノイズ \( \varepsilon \) は以下の正規分布に従うと仮定します。

\[ \varepsilon \sim \mathcal{N}(0, \sigma_n^2) \]

　このような観測データ \( \mathcal{D} = \{ (\bm{x}_i, y_i) \}_{i=1}^{n} \) が与えられると、ガウス過程回帰では新しい入力 \( \bm{x}^* \) に対する真の関数値 \( f(\bm{x}^*) \) の事後分布

\[ p\bigl(f(\bm{x}^*) \mid \bm{x}^*, \mathcal{D}\bigr) = \mathcal{N}\bigl(\mu(\bm{x}^*),\,\sigma^2(\bm{x}^*)\bigr) \]

を解析的に求めることができます。さらに、観測に独立同分布のノイズ \( \varepsilon \sim \mathcal{N}(0,\sigma_n^2) \) が乗ると仮定すれば、観測値 \( y(\bm{x}^*) = f(\bm{x}^*) + \varepsilon \) の分布は

\[ p\bigl(y(\bm{x}^*) \mid \bm{x}^*, \mathcal{D}\bigr) = \mathcal{N}\bigl(\mu(\bm{x}^*),\,\sigma^2(\bm{x}^*) + \sigma_n^2\bigr) \]

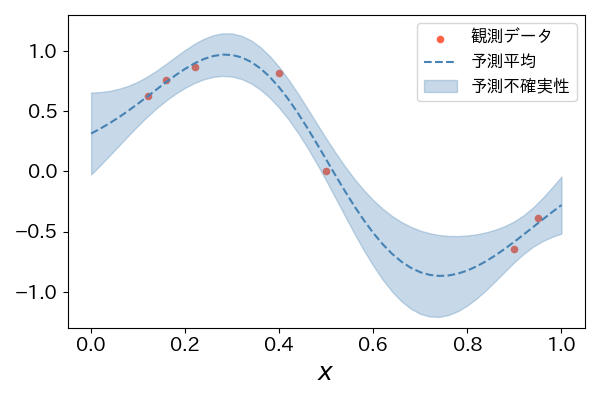
となります。ここで \( \mu(\bm{x}^*) \) は予測平均、\( \sigma^2(\bm{x}^*) \) は予測不確実性（モデルが推定した不確実性）を示し、後者はデータが乏しい領域や外挿の難易度が高い領域では値が大きくなる傾向があります（図1）。

　ベイズ最適化では、この「予測平均」と「予測不確実性」を組み合わせて 獲得関数を定義し、「次にどこを評価すべきか」を決定します。そのため、ガウス過程回帰はベイズ最適化の核となる代理モデルとして広く用いられています。

　獲得関数 (Acquisition Function) は、ベイズ最適化において「次に実験すべき点」を決めるために用いられる関数です。ガウス過程回帰によって得られた未知関数の事後分布（予測平均と予測不確実性）を利用して定義されます。獲得関数の値が大きいほど、その候補点が次の実験点として有望であることを意味します。

　代表的な獲得関数には以下があります。

• 期待改善量 (Expected Improvement; EI): 現在の最適な観測値からの改善量の期待値
• 改善確率量 (Probability of Improvement; PI): 現在の最適な観測値から改善する確率
• 信頼下限/上限 (Lower/Upper Confidence Bound; LCB/UCB): 事後分布の予測平均と予測不確実性を組み合わせたもの
  • 最小化問題では LCB: \( \mu(\bm{x}) -\sqrt{\beta}\sigma(\bm{x}) \) を、最大化問題では UCB: \( \mu(\bm{x}) +\sqrt{\beta}\sigma(\bm{x}) \) をそれぞれ使用します。ここで \( \beta \) は探索と活用のバランスを調整する正のハイパーパラメータです。
  • BoTorch では最大化問題が前提のため、主に UCB が使用されます。

　一般に、どの獲得関数についても探索と活用のトレードオフ (exploration-exploitation trade-off) を考慮します。「探索」は未知の条件を、「活用」は既知の良い評価点と似た条件を、それぞれ優先して調べることです。

　例えば、PI は現在の最適な観測値から改善するかしないかに焦点を当てる（改善量は気にしない）ため、活用の要素が強いといえます。一方、EI は予測不確実性をより考慮しており（確率が低くても大きく改善する場合も考慮）、活用と探索のバランスが取れているといえます。LCB/UCB は \( \beta \) の大きさによって探索と活用のバランスを調整します。

　ベイズ最適化では、この獲得関数を最大化する点を次の実験点として選択します。このように獲得関数を用いることで、限られた試行回数の中で効率的に目的関数の最適値を探索することが可能となります。

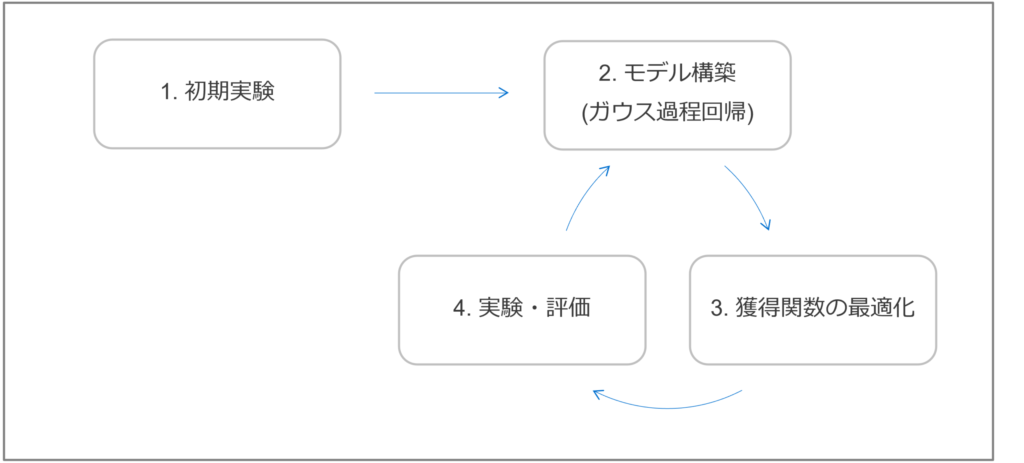
　ベイズ最適化は、目的関数を最大/最小にする最適解を効率的に探索するために、次のサイクルを繰り返すことが一般的です（図2のように手順 2～4 を繰り返す）。このサイクルによって、有望な領域に実験/計算リソースを集中させることができ、少ない試行回数で最適解に到達できます。

1. 初期実験: ベイズ最適化を始める前に少数の実験を行い、初期データを作成します。初期データ点の質や数は、その後の最適化効率に影響を与えるため重要です。初期点の選択方法としては、探索空間全体を網羅的にサンプリングするラテン超方格 (Latin Hypercube Sampling; LHS) や Sobol シーケンスなどがよく用いられます。
   • ランダムサンプリングに比べて、LHS や Sobol シーケンス は探索空間に偏りなく均一に点を配置する性質があります。これにより、最適化の初期段階で未知の関数形の全体像を効率的に把握しやすくなり、良い代理モデルを構築できます。
2. モデル構築（ガウス過程回帰）: 初期データとこれまでのサイクルで得られた観測データを全て用いて、ガウス過程回帰モデルを構築します。
3. 獲得関数の最適化: ガウス過程回帰モデルから得られる予測平均と予測不確実性を利用して獲得関数を計算します。この獲得関数を最大化する入力が、次の実験における最適な候補点となります。
4. 実験・評価: 得られた候補点に対して、実際に目的関数の値を観測する実験を行います。実験結果には観測ノイズが含まれることが一般的であり、ガウス過程回帰モデルはこの観測ノイズも考慮してモデル構築を行います。

　このサイクルを、事前に設定した最大実験回数に達するか、獲得関数の値が十分に小さくなるか、あるいは目的関数の値が収束したと判断されるまで繰り返します。サイクルを繰り返す度に、有望な領域のガウス過程回帰モデルはより正確になり、獲得関数は最適解の存在する可能性が高い領域をより的確に指し示すようになります。以上により、大域的な最適解を効率的に探索するのがベイズ最適化です。

　本章では、複数の目的を同時に最適化する多目的最適化について説明します。多目的ベイズ最適化は、ベイズ最適化の手法を多目的最適化に応用したものであるため、多目的最適化を理解しておくことは重要です。

　多目的最適化 (Multi-Objective Optimization; MOO) とは、複数の互いにトレードオフの関係にある目的関数を同時に最適化することです。具体的には、以下のような最適化問題として定式化されます。

\[ \max_{\bm{x} \in \mathcal{X}} \bm{F}(\bm{x}) = \max_{\bm{x} \in \mathcal{X}} (f_1(\bm{x}), f_2(\bm{x}), \ldots, f_M(\bm{x}))^{\mathrm{T}} \]

ここで、

• \( \bm{x} \) は探索空間 \( \mathcal{X} \) における探索点
• \( f_m(\bm{x}) \) は \( m \) 番目の目的関数 \( (m = 1, \ldots, M) \)
• \( \bm{F}(\bm{x}) \) は各目的関数を並べた \( M \) 次元のベクトル値関数

です。

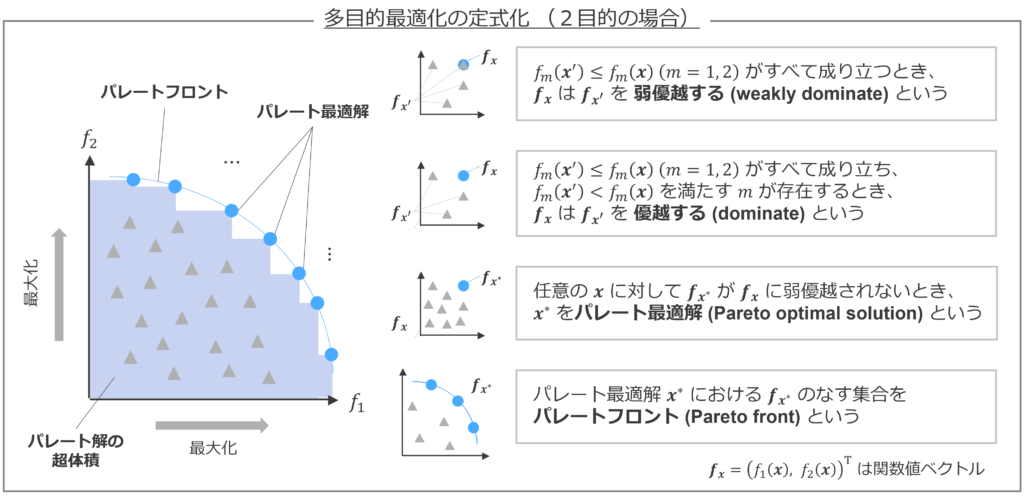
　単一の目的関数を最適化する場合とは異なり、多目的最適化においては全ての目的関数にとって同時に最良となる単一の解は一般には存在しません（トレードオフがあるからです）。

　よって、多目的最適化における解の評価には、解の優劣関係と呼ばれる二項関係を定義することが重要です。ある解 \( \bm{x}_1 \) が別の解 \( \bm{x}_2 \) を弱優越 (weakly dominate) するとは、全ての目的関数において \( \bm{x}_1 \) が \( \bm{x}_2 \) と同等以上の評価である場合を指します。一方、ある解 \( \bm{x}_1 \) が別の解 \( \bm{x}_2 \) を優越 (dominate) するとは、全ての目的関数において \( \bm{x}_1 \) が \( \bm{x}_2 \) 以上の評価であり、少なくとも一つの目的関数においては \( \bm{x}_1 \) が \( \bm{x}_2 \) より厳密に良い評価である場合を指します。

　そして、任意の解 \( \bm{x} \) から弱優越されない解 \( \bm{x}^* \) をパレート最適解 (Pareto Optimal Solution) と呼びます。パレート最適解たちを目的関数空間にプロットしたものはパレートフロント (Pareto Front) と呼ばれます（正しくは、パレート最適解たちによる目的関数値ベクトルの集合）。多数のパレート最適解を列挙してパレートフロントを推定することが多目的最適化の目標となります。

　言葉だけで理解するのはなかなか難しいため、図3も参考にしていただければ幸いです。

　多目的最適化を解く単純な方法として、各目的関数の重み付き和に対する単目的最適化（スカラー化）が考えられます。しかし、スカラー化ではパレート最適解が一つ得られるものの、一度の最適値探索で全てのパレート最適解が得られるわけではありません。よって、目的関数をスカラー化するのではなく、目的関数値ベクトルとして扱ったまま多目的最適化として解くことが一般的です（遺伝的アルゴリズムなど）。パレートフロントの性能評価には超体積 (Hypervolume) と呼ばれる指標がよく用いられます。

　超体積は、パレートフロントと目的関数空間上の参照点によって囲まれる空間の体積を表す指標です。最大化問題では、目的関数値が大きく、解の多様性が増加するほどパレートフロントの超体積は増加します。したがって、多目的最適化の進行に伴って超体積が増加していれば、パレートフロントも改善しているといえます。

　本章では、ベイズ最適化と多目的最適化を組み合わせた多目的ベイズ最適化について解説します。多目的ベイズ最適化は、評価にコストがかかる複数の目的関数を同時に最適化する問題に対して、非常に有効な手法です。特に、実験やシミュレーションなど、一度の評価に多くの時間やリソースを要する場合に効率的な最適解探索を実現します。

　多目的ベイズ最適化 (Multi-Objective Bayesian Optimization; MOBO) は、ブラックボックスの多目的関数を効率的に最適化するために、ベイズ最適化のフレームワークを適用したものです。単一目的のベイズ最適化と同様に、多目的ベイズ最適化も代理モデル（主にガウス過程回帰）を用いて目的関数の未知の関数形をモデル化し、多目的獲得関数を用いて次に評価すべき点を決定するというサイクルを繰り返します。

　単一目的のベイズ最適化と最も異なる点は、多目的獲得関数を用いることです。多目的獲得関数は、代理モデルから得られる各目的関数の予測情報を総合的に評価して、次に評価すべき点がパレートフロントの改善にどれだけ寄与するかを定量化します。例えば、既存のパレートフロントを基準として、新しい候補点を評価することで得られる期待超体積改善量 (Expected Hypervolume Improvement; EHVI) を最大化するアプローチが一般的で、これが EHVI と呼ばれる獲得関数です。このような獲得関数によって、単一の最適解ではなく、多様なパレート最適解を効率的に探索することが可能となります。

　多目的ベイズ最適化の最終的な出力は、単一の最適解ではなく、パレート最適解となります。このパレート最適解の中から、実務上の制約や意思決定者の好みに応じて、実際に使用する条件を選択することになります。

　本章では GPyTorch の実装について簡単に説明します。GPyTorch は深層学習ライブラリである PyTorch をベースとした、ガウス過程のためのライブラリです [5, 6] 。PyTorch と同じく Meta (旧 Facebook) AI Research によって開発されています。PyTorch をベースとしていることから、GPU を用いた高速演算やモデルの自動微分が可能となっており、非常に効率的にガウス過程回帰を実装することができます。

　公式ドキュメントによれば、以下のような特徴があります。

• 大幅な GPU アクセラレーション (MVM ベースの推論による)
• スケーラビリティと柔軟性を実現する最新のアルゴリズムの進歩の最先端の実装 (SKI/KISS-GP、確率的 Lanczos 展開、LOVE、SKIP、確率的変分深層カーネル学習など)
• 深層学習フレームワークとの簡単な統合

　GPyTorch の基本的な使い方については、公式ドキュメントに詳しい説明があります。特に、単一の目的関数に対するガウス過程回帰の実装例が分かりやすく解説されています。

　本記事では、多目的ベイズ最適化に焦点を当てるため、GPyTorch 単独の実装の詳細は割愛します。興味のある方は公式ドキュメントを参照してください。

　本章では BoTorch の実装について解説します。BoTorch は GPyTorch をベースとしたベイズ最適化のためのライブラリです [7]。PyTorch, GPyTorch と同じく Meta (旧 Facebook) AI Research によって開発されています。

　公式ドキュメントによれば、以下のような特徴があります（意訳）。

• ベイズ最適化の基本要素（確率モデル、獲得関数、オプティマイザーなど）を組み合わせるための使いやすいモジュールを提供
• 自動微分、GPU などのネイティブサポート、動的計算グラフなど、PyTorch の機能を最大限に活用
• 再パラメータ化トリックによりモンテカルロベースの獲得関数をサポートしており、厳しい制約を設けることなく新しいアイデアを簡単に試すことが可能
• PyTorch の深層学習や畳み込みニューラルネットワークとシームレスに連携可能
• GPyTorch の最先端の確率モデル（マルチタスクガウス過程、深層カーネル学習、深層ガウス過程、近似推論など）を完全にサポート

　現在、BoTorch はベータ版とされていますが、それでも活発に開発とメンテナンスが行われており、最新の研究成果が取り込まれやすく（後述する logEI はその典型例です）、信頼性の高いライブラリといえるでしょう。

　本記事では、BoTorch を用いた多目的ベイズ最適化の実装を、実際のコード例とともに詳しく解説していきます。ちなみに、BoTorch の発音は “bow-torch”（ボートーチ） です。

本記事では Python 3.12.10 を使用しています。また、主要なライブラリのバージョンは以下の通りです。

botorch==0.14.0
gpytorch==1.14
matplotlib==3.10.3
numpy==2.2.5
scikit-learn==1.6.1
scipy==1.15.3
torch==2.7.0

　本節では BoTorch の Get Started を題材として、BoTorch の使い方を簡単に解説していきます。なお、分かりやすさのために一部修正している箇所があります。

仮想データの作成

　仮想データを作成します。訓練データ train_X は 10 個の 2 次元データで、それぞれ \( [0, 1) \) の範囲で一様乱数として生成されています。また、入力 \( \bm{x} \) に対する関数 \( f \) を以下で定義します。これは、点 \( \bm{x} \) と点 \( (0.5, 0.5) \) のユークリッド距離が小さいほど \( 1 \) に近づく関数です。

\[ f(\bm{x}) = 1 -| \bm{x} -\mathbf{0.5} | \]

観測値 Y は 10 個の 1 次元データで、関数値に観測ノイズを加えた値となっています。

\[ y = f(\bm{x}) + \varepsilon \]

\[ \varepsilon \sim \mathcal{N}(0, 0.1^2) \]

ここで、観測ノイズ \( \varepsilon \) は平均が \( 0 \) で標準偏差が \( 0.1 \) の正規分布に従います。

import torch

train_X = torch.rand(10, 2, dtype=torch.double)
Y = 1 - torch.linalg.norm(train_X - 0.5, dim=-1, keepdim=True)
Y = Y + 0.1 * torch.randn_like(Y)  # add some noise

ガウス過程回帰モデルの構築

　ガウス過程回帰モデルを構築します。SingleTaskGP は、GPyTorch のガウス過程回帰モデルをラップした BoTorch のクラスで、BoTorch では基本的にこのようなクラスを使用します。前処理として、train_X には正規化 Normalize を、Y には標準化 Standardize をそれぞれ行っています。

　ExactMarginalLogLikelihood は GPyTorch のクラスで、ガウス過程回帰モデルの周辺対数尤度を計算します。ガウス過程回帰モデルはノンパラメトリックですが、例えば RBF カーネルにおける length scale のようなハイパーパラメータの値を決定する必要があります。このハイパーパラメータを訓練データにフィットさせるための一般的な方法の一つが、周辺対数尤度を最大化することです。この方法はエビデンス近似や第二種の最尤推定などと呼ばれます。

　fit_gpytorch_mll ではガウス過程回帰モデルのハイパーパラメータを訓練データにフィットさせます。内部的には scipy.optimize.minimize() で L-BFGS-B 法を用いた最適化が行われており、ここでは周辺対数尤度の最大化問題を解いていることになります。

from botorch.fit import fit_gpytorch_mll
from botorch.models import SingleTaskGP
from botorch.models.transforms import Normalize, Standardize
from gpytorch.mlls import ExactMarginalLogLikelihood

gp = SingleTaskGP(
    train_X=train_X,
    train_Y=Y,
    input_transform=Normalize(d=2),
    outcome_transform=Standardize(m=1),
)
mll = ExactMarginalLogLikelihood(gp.likelihood, gp)
fit_gpytorch_mll(mll)

獲得関数の定義

　獲得関数を定義します。最も広く使われている獲得関数の一つに期待改善量 (Expected Improvement; EI) があります。これに対して、2023 年に新しい獲得関数として logEI が提案されました [8]。logEI は EI の対数を取ったものとほぼ同じですが（詳細は [8] の式 (9) を確認してください）、対数を取ることで数値計算的な安定性を向上させており、勾配消失問題を緩和させて最適化のパフォーマンスを向上させています。そのような実装の一つが LogExpectedImprovement です（logEI 系の獲得関数は他にもあります）。

from botorch.acquisition import LogExpectedImprovement

logEI = LogExpectedImprovement(model=gp, best_f=Y.max())

　ちなみに、ExpectedImprovement を使用すると、以下のような Warning が出て、logEI を使用することが強く推奨されるようになっています。

NumericsWarning: ExpectedImprovement has known numerical issues that lead to suboptimal optimization performance. It is strongly recommended to simply replace

         ExpectedImprovement     -->     LogExpectedImprovement

instead, which fixes the issues and has the same API. See https://arxiv.org/abs/2310.20708 for details.
  legacy_ei_numerics_warning(legacy_name=type(self).__name__)

獲得関数の最適化

　獲得関数の最適化を行います。bounds によって入力 \( \bm{x} \) の探索範囲を \( [0, 1]^2 \) と指定しています。ここで、BoTorch の獲得関数（の最適化）には解析的なものと（Analytic, \( q=1 \)）モンテカルロベースのもの（MC-based, \( q>1 \)）の二種類があります。今回は単目的最適化ということもあり、解析的な獲得関数が使用されており候補点は一つしか得られません。一方、多目的ベイズ最適化の場合は MC ベースの獲得関数を使用して候補点を複数得たのち、最終的に人間が選択することが多いです。また、num_restarts 及び raw_samples を大きくすることでロバスト性が向上しますが計算負荷も増大します。なお、今回は乱数シードを固定していないため、print の結果は実行する度に変化します。

from botorch.optim import optimize_acqf

bounds = torch.stack([torch.zeros(2), torch.ones(2)]).to(torch.double)
candidate, acq_value = optimize_acqf(
    logEI, bounds=bounds, q=1, num_restarts=5, raw_samples=20,
)
print(candidate)  # tensor([[0.6504, 0.3316]], dtype=torch.float64)
print(acq_value)  # tensor(-3.9803, dtype=torch.float64)

　ここまでで Get Started の内容は終わりです。BoTorch の使い方は直感的で、非常に便利であることが分かったのではないかと思います。しかし、実務上はここまでシンプルではなく、ドメイン知識も活用しながらより複雑にカスタマイズしていくことになります。

　前節で BoTorch の使い方が理解できたら、BoTorch の公式ドキュメントにある Basic Concepts に目を通すことを強く推奨します（実はこの内容の一部を前節に盛り込んでいます）。

　Basic Concepts の主な内容は以下の通りです。

• モデル (Models): Multi-Output と Multi-Task、観測ノイズなどにおけるモデルの使い方
• 獲得関数 (Acquisition Functions): 解析的な獲得関数（\( q=1 \)）と MC ベースの獲得関数（\( q>1 \)）
• 最適化 (Optimization): ガウス過程回帰モデルのフィッティングと獲得関数の最適化

　BoTorch は、ガウス過程回帰やベイズ最適化に関わる背景知識を前提として設計されており、背景知識が不足していると BoTorch のリファレンスを読んでもピンと来ない場合があります。Basic Concepts は基本概念に加えて背景知識を学ぶヒントが得られるため一石二鳥です。

　本節では、BoTorch のチュートリアルを題材として、多目的ベイズ最適化の実装を解説します。

　チュートリアルではいくつかの獲得関数を用いた実装となっており読みにくいため、本記事では分かりやすさのために qNEHVI（実際は qlogNEHVI）だけを用いた実装に書き換えています。その上で、実務で使うことを想定した実装に書き換えて解説しています。ご了承ください。

dtype と device の指定

　dtype と device を指定します。torch.double は倍精度（64ビット）です。device では、GPU が使える場合は cuda を、そうでない場合は cpu を指定するようにしています。また、tkwargs は torch.tensor 等にキーワード引数として渡すための辞書となっています。

import torch

tkwargs = {
    "dtype": torch.double,
    "device": torch.device("cuda" if torch.cuda.is_available() else "cpu"),
}

問題設定

　本チュートリアルでは、多目的ベイズ最適化の問題設定として Branin-Currin 関数が使用されています。これらの関数は最適化アルゴリズムのベンチマークとしてよく用いられます。定義は以下の通りです。

Branin (rescaled):

\[
f(\bm{x}) = \left( 15 x_2 -\frac{5.1}{4 \pi^2} (15 x_1 -5)^2 + \frac{5}{\pi} (15 x_1 -5) -5 \right)^2 + \left( 10 -\frac{10}{8 \pi} \right) \cos(15 x_1 -5) \]

Currin:

\[ f(\bm{x}) = \left(1 -\exp\left(-\frac{1}{2 x_2}\right)\right) \left( \frac{2300 x_1^3 + 1900 x_1^2 + 2092 x_1 + 60}{100 x_1^3 + 500 x_1^2 + 4 x_1 + 20} \right) \]

ここで、\( \bm{x} = (x_1, x_2) \) です。目的関数が二つあるので多目的最適化の問題となっています。これにベイズ最適化を適用させることで、多目的ベイズ最適化の問題となります。

　これらは最小化問題の関数ですが、BoTorch では最大化問題が想定されています（チュートリアルにも記載があります）。よって、negate=True を指定することで符号反転して最大化問題に変換しています。

from botorch.test_functions.multi_objective import BraninCurrin

problem = BraninCurrin(negate=True).to(**tkwargs)

データの観測

　データの観測に対応する関数を定義します（チュートリアルにはない関数ですが、実務の想定に必要であるため作成しています）。これはあくまで仮想的なものであり、実務では現場で実験したりシミュレーションしたりしてデータを取得することになるため、シームレスに最適化ループを回すことにはならないことに注意が必要です。

　ここでは観測値（目的関数値）に観測ノイズが含まれます。観測ノイズは平均が \( (0,0) \) で標準偏差が \((15.19,0.63) \) の正規分布にそれぞれ従います。もちろん実務ではこのような観測ノイズの情報は未知であり、観測値やドメイン知識を活用しながら観測ノイズを推定することになります。

　また、観測ノイズが含まれない真値 obj_true も返すようになっていますが、実務では当然ながら真値を知ることはできず、観測ノイズが含まれる観測値 obj だけが得られます。本チュートリアルでなぜ真値も使っているのか筆者には分かりかねますが、恐らく分かりやすさのために観測値ではなく真値を使ったパレート解の超体積やパレートフロントの推移（後述）を示すためだと考えられます。

　ちなみに、obj は目的関数 (Objective Function) から取った名前で、最適化の実装では慣例的によく使用されます。

# 各目的関数値に対する観測ノイズの値（標準偏差）
NOISE_SE = torch.tensor([15.19, 0.63], **tkwargs)

def observe_data(x):
    """x.shape=(n,2)"""
    obj_true = problem(x)  # 真値
    obj = obj_true + torch.randn_like(obj_true) * NOISE_SE  # 観測値
    return obj, obj_true

初期データの作成

　初期データを作成します。ここでは 6 個の初期データを生成しています。初期データの作成は初期実験とも呼ばれ、実務でも重要な意味を持ちます。一般に初期実験では実験計画法を用いて様々なパターンのデータを作成するのがセオリーとなっています。本チュートリアルでは Sobol シーケンスという手法が用いられており、乱数よりも空間を均一に埋めるようなサンプリングを行う性質を持ちます。

from botorch.utils.sampling import draw_sobol_samples

N_INIT_DATA = 6

train_x = draw_sobol_samples(bounds=problem.bounds, n=N_INIT_DATA, q=1).squeeze(1)  # shape=(6,2)
train_obj, train_obj_true = observe_data(train_x)

ガウス過程回帰モデルの初期化

　ガウス過程回帰モデルを初期化する関数を定義します。今回は目的関数が二つあるため、二つのガウス過程回帰モデルを作成して ModelListGP でまとめています。これは独立性を仮定して別々にモデリングしているということでもあります。逆に、相関（共分散）を考慮したい場合は多出力ガウス過程回帰 (Multi-Output Gaussian Process) を使用します。これは目的関数間に相関がある場合により正確なモデリングが可能になるというメリットがあります。multi-output なモデリングは GPyTorch と BoTorch でサポートされていますので、興味がある方は調べてみてください（GPyTorch の公式ドキュメント）。

　また、train_yvar によって各目的関数値に対する観測ノイズの値が直接的に与えられていますが、実務では初期データが少ない中でこのように観測ノイズが正確に分かることはないでしょう。ただ、似たような問題設定の経験があれば、そのドメイン知識から標準偏差の値をある程度見積もることは可能です。その場合でも、標準偏差の値を直接指定するのではなく範囲制約を与える方が筋がよいでしょう。詳細は省略しますが、そのような制約は GPyTorch の機能を使うことで実現できます。

　なお、SingleTaskGP は train_yvar を指定することで train_yvar を固定ノイズとして取り扱います。実務では train_yvar を指定せず、等分散性 (Homoskedastic) を仮定して観測ノイズを推定させるのがよいでしょう。詳しくは公式ドキュメントを参照してください。

from botorch.models.gp_regression import SingleTaskGP
from botorch.models.model_list_gp_regression import ModelListGP
from botorch.models.transforms.outcome import Standardize
from gpytorch.mlls.sum_marginal_log_likelihood import SumMarginalLogLikelihood
from botorch.utils.transforms import unnormalize, normalize

def initialize_model(train_x, train_obj):
    """ガウス過程回帰モデルを初期化する."""
    train_x = normalize(train_x, problem.bounds)  # 正規化
    models = []
    # 目的関数ごとにガウス過程回帰モデルを作成
    for i in range(train_obj.shape[-1]):
        train_y = train_obj[..., i : i + 1]  # shape=(n,1)
        train_yvar = torch.full_like(train_y, NOISE_SE[i] ** 2)
        model = SingleTaskGP(train_x, train_y, train_yvar, outcome_transform=Standardize(m=1))
        models.append(model)
    model = ModelListGP(*models)
    mll = SumMarginalLogLikelihood(model.likelihood, model)
    return mll, model

獲得関数の最適化と候補点の観測

　獲得関数の最適化と候補点の観測を行う関数を定義します。ここでは獲得関数として qlogNEHVI (q-Log Noisy Expected Hypervolume Improvement) を使用しています。これは MC ベースの獲得関数であり、前述した logEI 系の獲得関数であり [8]、観測ノイズを考慮した EHVI でもあります。

　ref_point はパレート解の超体積 (Hypervolume) を計算するために必要な参照点です。具体的には、最大化問題においてパレート解の超直方体を構成するための下限値を定める点です。ここでは problem.ref_point を使用することで理想的な参照点を設定していますが、実際はドメイン知識を用いて目的関数値の下限値から少し小さい値に設定するのがよいでしょう。下限値がよく分かっていない場合は、現時点の最小値から十分小さい値に設定しておけばよいです。

　ここでは候補点の数は 4 個としており、その後に 4 個とも観測をしています。実務では候補点の数を多めに設定して多目的ベイズ最適化を実行し、トレードオフを考慮しながら実際に実験する点を人間が選択することになります。

from botorch.optim.optimize import optimize_acqf
from botorch.acquisition.multi_objective.logei import qLogNoisyExpectedHypervolumeImprovement

BATCH_SIZE = 4     # 候補点の数
NUM_RESTARTS = 10  # 多スタート獲得関数の最適化の開始点の数（並列実行数）
RAW_SAMPLES = 512  # 初期点のサンプリング数

standard_bounds = torch.zeros(2, problem.dim, **tkwargs)
standard_bounds[1] = 1
# tensor([[0., 0.],
#         [1., 1.]], dtype=torch.float64)

def optimize_qlognehvi_and_get_observation(model, train_x, sampler):
    """獲得関数 qlogNEHVI の最適化を行い、候補点とその観測値を返す."""
    # 獲得関数 qlogNEHVI の定義
    acq_func = qLogNoisyExpectedHypervolumeImprovement(
        model=model,
        ref_point=problem.ref_point.tolist(),
        X_baseline=normalize(train_x, problem.bounds),
        prune_baseline=True,
        sampler=sampler,
    )
    # 獲得関数 qlogNEHVI の最適化
    candidates, _ = optimize_acqf(
        acq_function=acq_func,
        bounds=standard_bounds,
        q=BATCH_SIZE,
        num_restarts=NUM_RESTARTS,
        raw_samples=RAW_SAMPLES,
        options={"batch_limit": 5, "maxiter": 200},
        sequential=True,
    )
    # 候補点の観測
    new_x = unnormalize(candidates.detach(), bounds=problem.bounds)
    new_obj, new_obj_true = observe_data(new_x)
    return new_x, new_obj, new_obj_true

多目的ベイズ最適化のループ

　多目的ベイズ最適化のループを回します。ここでは N_BATCH = 20 として 20 回の最適化ループをシームレスに回すようになっていますが、「データの観測」で前述した通り、実務では各ループにおいて現場で実験したりシミュレーションしたりしてデータを取得することになります。

　関数 update_hypervolume() ではパレート解の超体積を更新しています。超体積の計算は獲得関数の最適化 optimize_acqf の中で行われるため、明示的に計算する必要はありませんが、ここでは最適化ループが進むにつれて超体積がどのように改善しているかを可視化するために計算しています。

　最適化ループの中では、ガウス過程回帰モデルの構築、獲得関数の最適化、候補点の観測を行っています。まずガウス過程回帰モデルを初期化し、fit_gpytorch_mll でハイパーパラメータを訓練データにフィットさせます。また、GPyTorch のチュートリアルにもある通り、PyTorch の学習ループを自分自身で書くことも可能です。この方法では、Adam などのオプティマイザーを使ったり、学習率スケジューリングをしたりなどの細かいカスタマイズが可能になります。fit_gpytorch_mll でガウス過程回帰モデルのフィッティングが思うようにいかない場合にはこの方法を試すのがよいでしょう。

　SobolQMCNormalSampler は MC ベースの獲得関数に使用するサンプラーです。詳細は公式ドキュメントを参照してください。

　最後に、獲得関数の最適化と候補点の観測を行います。その後、得られた候補点の観測データを新たに訓練データに追加し、次の最適化ループへと進んでいきます。

import time
import warnings

from botorch import fit_gpytorch_mll
from botorch.exceptions import BadInitialCandidatesWarning
from botorch.sampling.normal import SobolQMCNormalSampler
from botorch.utils.multi_objective.box_decompositions.dominated import DominatedPartitioning

warnings.filterwarnings("ignore", category=BadInitialCandidatesWarning)
warnings.filterwarnings("ignore", category=RuntimeWarning)

N_BATCH = 20      # 多目的ベイズ最適化のループ回数
MC_SAMPLES = 128  # 増やすと獲得関数の近似精度が向上するが計算時間も増加

hvs_list = []
def update_hypervolume():
    """パレート解の超体積を更新する."""
    bd = DominatedPartitioning(ref_point=problem.ref_point, Y=train_obj_true)
    volume = bd.compute_hypervolume().item()
    hvs_list.append(volume)

# 初期データによるパレート解の超体積
update_hypervolume()

# N_BATCH 回の多目的ベイズ最適化
for iteration in range(1, N_BATCH + 1):
    t0 = time.monotonic()

    # ガウス過程回帰モデルの初期化
    mll, model = initialize_model(train_x, train_obj)

    # ガウス過程回帰モデルのハイパーパラメータを訓練データにフィットさせる
    fit_gpytorch_mll(mll)

    # MCベースの獲得関数に使用するサンプラー
    sampler = SobolQMCNormalSampler(sample_shape=torch.Size([MC_SAMPLES]))

    # 獲得関数 qlogNEHVI の最適化を行い、候補点とその観測値を得る
    new_x, new_obj, new_obj_true = optimize_qlognehvi_and_get_observation(model, train_x, sampler)

    # 観測点を訓練データに追加する
    train_x = torch.cat([train_x, new_x])
    train_obj = torch.cat([train_obj, new_obj])
    train_obj_true = torch.cat([train_obj_true, new_obj_true])

    # パレート解の超体積を更新
    update_hypervolume()

    t1 = time.monotonic()
    print(f"\nBatch {iteration:>2}: Hypervolume = {hvs_list[-1]:>4.2f}, time = {t1-t0:>4.2f}.", end="")

Batch  1: Hypervolume = 2.37, time = 7.38.
Batch  2: Hypervolume = 29.38, time = 5.78.
Batch  3: Hypervolume = 39.38, time = 8.75.
Batch  4: Hypervolume = 46.08, time = 10.36.
Batch  5: Hypervolume = 48.93, time = 8.28.
Batch  6: Hypervolume = 51.69, time = 9.33.
Batch  7: Hypervolume = 51.90, time = 14.12.
Batch  8: Hypervolume = 52.60, time = 16.44.
Batch  9: Hypervolume = 53.85, time = 19.61.
Batch 10: Hypervolume = 54.15, time = 20.19.
Batch 11: Hypervolume = 55.91, time = 31.83.
Batch 12: Hypervolume = 56.21, time = 20.55.
Batch 13: Hypervolume = 56.56, time = 25.59.
Batch 14: Hypervolume = 56.66, time = 30.59.
Batch 15: Hypervolume = 56.69, time = 23.88.
Batch 16: Hypervolume = 56.69, time = 36.42.
Batch 17: Hypervolume = 56.69, time = 43.72.
Batch 18: Hypervolume = 56.69, time = 41.56.
Batch 19: Hypervolume = 56.69, time = 30.89.
Batch 20: Hypervolume = 56.69, time = 52.11.

パレート解の超体積の推移

　パレート解の超体積の推移を可視化します。ここでは真のパレート解の超体積（つまり最大値） problem.max_hv が既知であることを仮定して、その差分値の対数を取っています。多目的ベイズ最適化のループを回していくにつれて、パレート解の超体積が増加して最大値に近づいている（差分値がゼロに近づいている）ことが分かります。

import numpy as np
from matplotlib import pyplot as plt

iters = np.arange(N_BATCH + 1) * BATCH_SIZE
log_hv_difference = np.log10(problem.max_hv - np.asarray(hvs_list))

fig, ax = plt.subplots(1, 1, figsize=(6, 4))
ax.errorbar(iters, log_hv_difference, label="qNEHVI", linewidth=1.5)
ax.set(xlabel="number of observations (beyond initial points)",
       ylabel="Log Hypervolume Difference")
ax.legend(loc="lower left")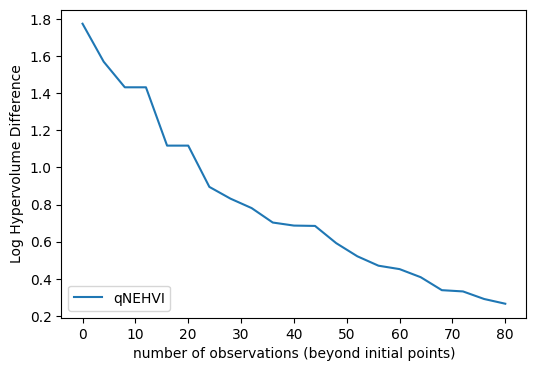

パレートフロントの推移

　パレートフロントの推移を可視化します。これだけだと少し分かりにくいですが、20 回の最適化で十分なパレートフロントが得られていることが分かります。なお、初期データを 6 個作成しており、1 回の最適化で 4 個の候補点を観測しているため、最終的に \( 6 + 4 \times 20 = 86 \) 個のデータを観測しています。

from matplotlib.cm import ScalarMappable

fig, ax = plt.subplots(figsize=(5, 5))
cm = plt.get_cmap("viridis")

batch_number = np.concatenate([
    np.zeros(N_INIT_DATA),
    np.arange(1, N_BATCH + 1).repeat(BATCH_SIZE),
])

sc = ax.scatter(
    train_obj_true[:, 0].cpu().numpy(),
    train_obj_true[:, 1].cpu().numpy(),
    c=batch_number,
    alpha=0.8,
)
ax.set_title("qNEHVI", fontsize=14)
ax.set_xlabel("Objective 1", fontsize=12)
ax.set_ylabel("Objective 2", fontsize=12)
norm = plt.Normalize(batch_number.min(), batch_number.max())
sm = ScalarMappable(norm=norm, cmap=cm)
sm.set_array([])
fig.subplots_adjust(right=0.85)
cbar_ax = fig.add_axes([0.93, 0.15, 0.02, 0.7])
cbar = fig.colorbar(sm, cax=cbar_ax)
cbar.ax.set_title("Iteration")

　パレートフロント付近を拡大して 10 回ずつに分けて可視化すると以下のようになります。10 回の時点でパレートフロントの概形がほぼ分かるようになっていますが、20 回まで行うことで多様性が増していることが分かります。この多様性の増加は、パレート解の超体積の増加と対応しています。

fig, ax = plt.subplots(figsize=(5, 5))

labels = [f"{N_INIT_DATA + BATCH_SIZE * (N_BATCH // 2 * i)} observations" for i in range(3)]
sc = ax.scatter(
    train_obj_true[:N_INIT_DATA, 0].cpu().numpy(),
    train_obj_true[:N_INIT_DATA, 1].cpu().numpy(),
    alpha=0.5,
    label=labels[0],
)
sc = ax.scatter(
    train_obj_true[N_INIT_DATA: N_INIT_DATA + BATCH_SIZE * N_BATCH // 2, 0].cpu().numpy(),
    train_obj_true[N_INIT_DATA: N_INIT_DATA + BATCH_SIZE * N_BATCH // 2, 1].cpu().numpy(),
    alpha=0.5,
    label=labels[1],
)
sc = ax.scatter(
    train_obj_true[N_INIT_DATA + BATCH_SIZE * N_BATCH // 2:, 0].cpu().numpy(),
    train_obj_true[N_INIT_DATA + BATCH_SIZE * N_BATCH // 2:, 1].cpu().numpy(),
    alpha=0.5,
    label=labels[2],
)
ax.set_title("qNEHVI", fontsize=14)
ax.set_xlabel("Objective 1", fontsize=12)
ax.set_ylabel("Objective 2", fontsize=12)
ax.set_xlim(-55, 15)
ax.set_ylim(-8, 1)
ax.legend()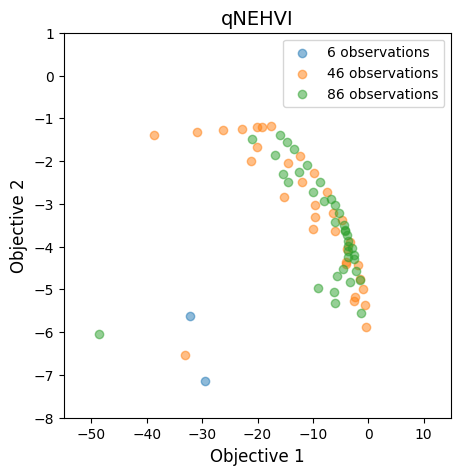

　ここまででチュートリアルの内容は終わりです。BoTorch を用いた多目的ベイズ最適化の基本的な流れが理解できたのではないかと思います。Get Started からの繰り返しになりますが、実務ではドメイン知識も活用しながらより複雑にカスタマイズしていくことになります。

　本記事では、多目的ベイズ最適化の基礎から実装までを解説しました。ベイズ最適化と多目的最適化の説明から始まり、それらを組み合わせた手法である多目的ベイズ最適化の説明を行い、GPyTorch と BoTorch を用いた多目的ベイズ最適化の具体的なコード例を示しながら解説を行いました。

　本記事の内容を理解することによって、多目的ベイズ最適化の基本的な考え方を理解して GPyTorch と BoTorch を使った実装の入り口に立ったり、実務で多目的最適化問題に直面した際の選択肢として多目的ベイズ最適化を検討できるようになったりすることが期待できます。

　本記事を足掛かりに、必要に応じて GPyTorch と BoTorch の公式ドキュメントを読んでいただき、より実践的な多目的ベイズ最適化に繋がっていけば幸いです。

参考文献